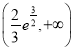题目内容
【题目】2016年9月,第22届鲁台经贸洽谈会在潍坊鲁台会展中心举行,在会展期间某展销商销售一种商品,根据市场调查,每件商品售价![]() (元)与销量
(元)与销量![]() (万件)之间的函数关系如图所示,又知供货价格与销量成反比,比例系数为20.(注:每件产品利润=售价-供货价格)
(万件)之间的函数关系如图所示,又知供货价格与销量成反比,比例系数为20.(注:每件产品利润=售价-供货价格)

(Ⅰ)求售价15元时的销量及此时的供货价格;
(Ⅱ)当销售价格为多少时总利润最大,并求出最大利润.
【答案】(Ⅰ)![]() ;(Ⅱ)当销售价格为
;(Ⅱ)当销售价格为![]() 元时,总利润最大,最大为
元时,总利润最大,最大为![]() 万元
万元
【解析】
试题(Ⅰ)由所给图像可知,销量和价格的图像是一条直线,设函数为![]() ,代入两点,可得直线方程
,代入两点,可得直线方程![]() ,当
,当![]() 时,
时,![]() ,又因为供货价格与销量呈反比,所以设
,又因为供货价格与销量呈反比,所以设![]() ,这样当
,这样当![]() 时可求得供货价格为4;(Ⅱ)根据(Ⅰ)的结果,可得供货价格与售价的函数关系
时可求得供货价格为4;(Ⅱ)根据(Ⅰ)的结果,可得供货价格与售价的函数关系![]() ,这样根据利润关系可得函数为
,这样根据利润关系可得函数为![]() ,这样可转换为二次函数求最值.
,这样可转换为二次函数求最值.
试题解析:(Ⅰ)由图知每件商品的售价与销量之间的函数关系为一次函数,设![]() ,
,
则![]() ,即
,即![]()
![]() ,
, ![]() .
.
![]() 售价为
售价为![]() 元时,销量为
元时,销量为![]() 万件.
万件.
又供货价格与销量成反比,比例系数为![]() ,
,
![]() 此时的供货价格为
此时的供货价格为![]() 元.
元.
(Ⅱ)由图知![]() ,
,
![]() 商品供货价格为
商品供货价格为![]() ,
,
![]() 销售商品的总利润
销售商品的总利润![]() ,
,
![]() 当销售价格为
当销售价格为![]() 元时,总利润最大,最大为
元时,总利润最大,最大为![]() 万元.
万元.

 金钥匙试卷系列答案
金钥匙试卷系列答案【题目】某校![]() 位同学的数学与英语成绩如下表所示:
位同学的数学与英语成绩如下表所示:
学号 |
|
|
|
|
|
|
|
|
|
|
数学成绩 |
|
|
|
|
|
|
|
|
|
|
英语成绩 |
|
|
|
|
|
|
|
|
|
|
学号 |
|
|
|
|
|
|
|
|
|
|
数学成绩 |
|
|
|
|
|
|
|
|
|
|
英语成绩 |
|
|
|
|
|
|
|
|
|
|
将这![]() 位同学的两科成绩绘制成散点图如下:
位同学的两科成绩绘制成散点图如下:
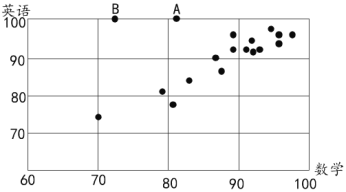
(1)根据该校以往的经验,数学成绩![]() 与英语成绩
与英语成绩![]() 线性相关.已知这
线性相关.已知这![]() 名学生的数学平均成绩为
名学生的数学平均成绩为![]() ,英语平均成绩为
,英语平均成绩为![]() .考试结束后学校经过调查发现学号为
.考试结束后学校经过调查发现学号为![]() 的
的![]() 同学与学号为
同学与学号为![]() 的
的![]() 同学(分别对应散点图中的
同学(分别对应散点图中的![]() 、
、![]() )在英语考试中作弊,故将两位同学的两科成绩取消,取消两位作弊同学的两科成绩后,求其余同学的数学成绩与英语成绩的平均数;
)在英语考试中作弊,故将两位同学的两科成绩取消,取消两位作弊同学的两科成绩后,求其余同学的数学成绩与英语成绩的平均数;
(2)取消两位作弊同学的两科成绩后,求数学成绩![]() 与英语成绩
与英语成绩![]() 的线性回归方程
的线性回归方程![]() ,并据此估计本次英语考试学号为
,并据此估计本次英语考试学号为![]() 的同学如果没有作弊的英语成绩(结果保留整数).
的同学如果没有作弊的英语成绩(结果保留整数).
附:![]() 位同学的两科成绩的参考数据:
位同学的两科成绩的参考数据:![]() ,
,![]() .
.
参考公式: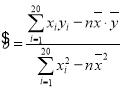 ,
,![]() .
.