题目内容
【题目】设函数![]() ,已知方程
,已知方程![]() (
(![]() 为常数)在
为常数)在![]() 上恰有三个根,分别为
上恰有三个根,分别为![]() ,下述四个结论:
,下述四个结论:
①当![]() 时,
时,![]() 的取值范围是
的取值范围是![]() ;
;
②当![]() 时,
时,![]() 在
在![]() 上恰有2个极小值点和1个极大值点;
上恰有2个极小值点和1个极大值点;
③当![]() 时,
时,![]() 在
在![]() 上单调递增;
上单调递增;
④当![]() 时,
时,![]() 的取值范围为
的取值范围为![]() ,且
,且![]()
其中正确的结论个数为( )
A.1B.2C.3D.4
【答案】C
【解析】
利用三角函数的图象和性质,对每一个命题逐一分析判断得解.
①当![]() 时,
时,![]() ,令
,令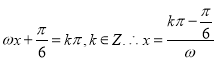 .
.
当![]() 时,
时, ;当
;当![]() 时,
时, ;
;
所以![]() ,所以
,所以![]() .所以该命题是正确的;
.所以该命题是正确的;
②当![]() 时, 令
时, 令 ,
,
当![]() 时,
时,![]() 令
令![]()
当![]() 时,
时,![]() 令
令![]()
因为![]() ,
,
所以![]() 在
在![]() 上有两个极大值点,所以该命题是错误的;
上有两个极大值点,所以该命题是错误的;
③当![]() 时,令
时,令 .
.
所以函数的单调递增区间为
当![]() 时,
时,![]() ,
,
因为![]() ,所以
,所以![]() ,
,
因为![]() ,所以当
,所以当![]() 时,
时,![]() 在
在![]() 上单调递增.
上单调递增.
所以该命题正确;
④当![]() 时,
时,![]() ,因为
,因为![]() 所以
所以
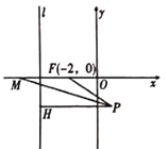
![]() ,设
,设![]() ,如图所示,当
,如图所示,当![]() 时,直线
时,直线![]() 和函数的图象有三个交点.此时
和函数的图象有三个交点.此时![]() .
.

所以![]() 所以
所以![]() .所以该命题正确.
.所以该命题正确.
故选:![]()

练习册系列答案
相关题目
【题目】有一项针对我国《义务教育数学课程标准》的研究,表1为各个学段每个内容主题所包含的条目数.下图是将下表的条目数转化为百分比,按各学段绘制的等高条形图.由图表分析得出以下四个结论,其中错误的是( )
学段 内容主题 | 第一学段 (1—3年级) | 第二学段 (4—6年级) | 第三学段 (7—9年级) | 合计 |
数与代数 | 21 | 28 | 49 | 98 |
图形与几何 | 18 | 25 | 87 | 130 |
统计与概率 | 3 | 8 | 11 | 22 |
综合与实践 | 3 | 4 | 3 | 10 |
合计 | 45 | 65 | 150 | 260 |
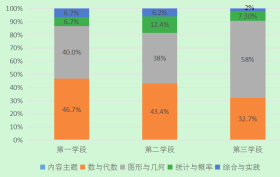
A.除了“综合与实践”外,其他三个内容领域的条目数都随着学段的升高而增加,尤其“图形与几何”在第三学段急剧增加,约是第二学段的3.5倍
B.在所有内容领域中,“图形与几何”内容最多,占![]() .“综合与实践”内容最少,约占
.“综合与实践”内容最少,约占![]()
C.第一、二学段“数与代数”内容最多,第三学段“图形与几何”内容最多
D.“数与代数”内容条目数虽然随着学段的增长而增长,而其百分比却一直在减少.“图形与几何”内容条目数,百分比都随学段的增长而增长