题目内容
【题目】已知函数 (
(![]() 且a为常数)和
且a为常数)和![]() (
(![]() 且k为常数),有以下命题:①当
且k为常数),有以下命题:①当![]() 时,函数
时,函数![]() 没有零点;②当
没有零点;②当![]() 时,若
时,若![]() 恰有3个不同的零点
恰有3个不同的零点![]() ,则
,则![]() ;③对任意的
;③对任意的![]() ,总存在实数
,总存在实数![]() ,使得
,使得![]() 有4个不同的零点
有4个不同的零点![]() ,且
,且![]() 成等比数列.其中的真命题是_____(写出所有真命题的序号)
成等比数列.其中的真命题是_____(写出所有真命题的序号)
【答案】②
【解析】
①根据题意,将函数的零点个数问题,转换为对应函数图像的交点个数问题,分别判断![]() ,
,![]() 两种情况下,函数零点的个数情况,即可判断出结果;
两种情况下,函数零点的个数情况,即可判断出结果;
②根据题意,先令![]() ,画出函数
,画出函数![]() 的图像,结合函数零点个数以及函数图像,判断方程
的图像,结合函数零点个数以及函数图像,判断方程![]() 根的分布情况,以及方程
根的分布情况,以及方程![]() 根的个数情况,即可判断出结果;
根的个数情况,即可判断出结果;
③根据题意,只需判断出![]() 时,函数零点个数不一定是
时,函数零点个数不一定是![]() 个,即可得出结果.
个,即可得出结果.
①因为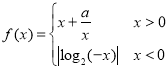 ,
,![]() ,由
,由![]() 得,函数
得,函数![]() 的零点,即是函数
的零点,即是函数![]() 图像与直线
图像与直线![]() 交点的横坐标,
交点的横坐标,
当![]() 时,
时,![]() 恒成立,因为
恒成立,因为![]() ,所以
,所以![]() 时,函数
时,函数![]() 显然没有零点;
显然没有零点;
当![]() 时,由
时,由![]() 得
得![]() ,即
,即![]() ,即
,即![]() ,
,
因为![]() ,所以
,所以![]() 恒成立,若
恒成立,若![]() 时,函数
时,函数![]() 可能有零点;若
可能有零点;若![]() ,函数
,函数![]() 没有零点;故①错;
没有零点;故①错;
②当![]() 时,因为
时,因为![]() 恰有
恰有![]() 个不同零点,令
个不同零点,令![]() ,则关于
,则关于![]() 的方程
的方程![]() 有两个不同的实数解,记作
有两个不同的实数解,记作![]() ,不妨令
,不妨令![]() ;
;
做出函数![]() 的图像如下:
的图像如下:
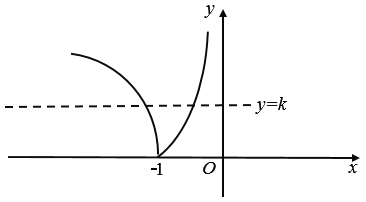
由图像可得:当![]() 时,
时,![]() 与
与![]() 有
有![]() 个交点;
个交点;
当![]() 时,
时,![]() 与
与![]() 有
有![]() 个交点;
个交点;
因为函数![]() 恰有
恰有![]() 个不同零点,
个不同零点,
则![]() 有
有![]() 个根,记作
个根,记作![]() ;
;![]() 有
有![]() 个根,记作
个根,记作![]() (不妨令
(不妨令![]() );
);
所以只需![]() ,
,![]() ,因此
,因此![]() ,
,![]() ,
,
所以![]() ;
;![]() ,
,![]() ,因此
,因此![]() ;故②正确;
;故②正确;
③由![]() ,得
,得![]() ;
;
所以函数![]() 与
与![]() 图像交点个数,即为函数
图像交点个数,即为函数![]() 的零点个数;
的零点个数;
由②中图像可知:当![]() 时,
时,![]() 与
与![]() 在
在![]() 上有
上有![]() 个交点,即函数
个交点,即函数![]() 在
在![]() 上有
上有![]() 个零点;
个零点;
当![]() 时,若
时,若![]() ,则函数
,则函数![]() 在
在![]() 上单调递增,因此函数
上单调递增,因此函数![]() 与
与![]() 在
在![]() 上最多只有
上最多只有![]() 个交点,即函数
个交点,即函数![]() 在
在![]() 上最多只有
上最多只有![]() 个零点;不满足存在实数
个零点;不满足存在实数![]() ,使得
,使得![]() 有4个不同的零点;
有4个不同的零点;
若![]() ,由基本不等式可得:
,由基本不等式可得:![]() ,即
,即![]() 时,
时,![]() ;
;
若![]() ,则函数
,则函数![]() 与
与![]() 在
在![]() 上最多只有
上最多只有![]() 个交点,也不满足对任意的
个交点,也不满足对任意的![]() ,总存在实数
,总存在实数![]() ,使得
,使得![]() 有4个不同的零点.故③错.
有4个不同的零点.故③错.
故答案为:②.

【题目】随着新高考改革的不断深入,高中学生生涯规划越来越受到社会的关注.一些高中已经开始尝试开设学生生涯规划选修课程,并取得了一定的成果.如表为某高中为了调查学生成绩与选修生涯规划课程的关系,随机抽取50名学生的统计数据.
成绩优秀 | 成绩不够优秀 | 总计 | |
选修生涯规划课 | 15 | 10 | 25 |
不选修生涯规划课 | 6 | 19 | 25 |
总计 | 21 | 29 | 50 |
(1)根据列联表运用独立性检验的思想方法能否有99%的把握认为“学生的成绩是否优秀与选修生涯规划课有关”,并说明理由;
(2)现用分层抽样的方法在选修生涯规划课的成绩优秀和成绩不够优秀的学生中随机抽取5名学生作为代表,从5名学生代表中再任选2名学生继续调查,求这2名学生成绩至少有1人优秀的概率.
参考附表:
P(K2≥k) | 0.100 | 0.050 | 0.010 | 0.001 |
k | 2.706 | 3.841 | 6.635 | 10.828 |
参考公式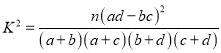 ,其中n=a+b+c+d.
,其中n=a+b+c+d.
【题目】随着新高考改革的不断深入,高中学生生涯规划越来越受到社会的关注.一些高中已经开始尝试开设学生生涯规划选修课程,并取得了一定的成果.下表为某高中为了调查学生成绩与选修生涯规划课程的关系,随机抽取50名学生的统计数据.
成绩优秀 | 成绩不够优秀 | 总计 | |
选修生涯规划课 | 15 | 10 | 25 |
不选修生涯规划课 | 6 | 19 | 25 |
总计 | 21 | 29 | 50 |
(Ⅰ)根据列联表运用独立性检验的思想方法能否有![]() 的把握认为“学生的成绩是否优秀与选修生涯规划课有关”,并说明理由;
的把握认为“学生的成绩是否优秀与选修生涯规划课有关”,并说明理由;
(Ⅱ)如果从全校选修生涯规划课的学生中随机地抽取3名学生,求抽到成绩不够优秀的学生人数![]() 的分布列和数学期望(将频率当作概率计算).
的分布列和数学期望(将频率当作概率计算).
参考附表:
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
参考公式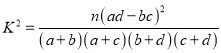 ,其中
,其中![]() .
.