题目内容
【题目】甲、乙二人进行一场比赛，该比赛采用三局两胜制，即先获得两局胜利者获得该场比赛胜利.在每一局比赛中，都不会出现平局，甲获胜的概率都为
.
（1）求甲在第一局失利的情况下，反败为胜的概率；
（2）若
，比赛结束时，设甲获胜局数为
，求其分布列和期望
；
（3）若甲获得该场比赛胜利的概率大于甲每局获胜的概率，求
的取值范围.
【答案】（1）
；（2）详见解析；（3）
.
【解析】
（1）设
甲在第一局失利，
甲获得了比赛的胜利，利用条件概率的概率公式可求得所求事件的概率；
（2）根据题意可知随机变量
的可能取值为
、
、
，计算出随机变量在不同取值下的概率，列出分布列，进而可计算出随机变量的数学期望；
（3）计算出甲获得该场比赛的概率，根据题意得出关于
的不等式，即可解得的取值范围.
（1）设甲在第一局失利，甲获得了比赛的胜利，则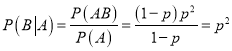
；
（2）由题意可知，随机变量的可能取值为、、，
则
，
，
.
随机变量的分布列如下：
|
|
|
|
|
|
|
|
则
；
（3）甲获得该场比赛胜利的概率为
，则
.
即
，解得
，所以的取值范围是.
练习册系列答案
相关题目
