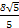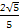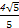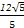题目内容
在△ABC中,已知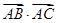 =3
=3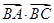 .
.
(1)求证:tan B=3tan A;
(2)若cos C=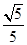 ,求A的值.
,求A的值.
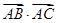 =3
=3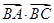 .
.(1)求证:tan B=3tan A;
(2)若cos C=
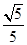 ,求A的值.
,求A的值.(1)见解析(2)A=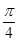
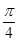
(1)因为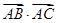 =3
=3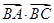 ,所以AB·AC·cos A=3BA·BC·cos B,
,所以AB·AC·cos A=3BA·BC·cos B,
即AC·cos A=3BC·cos B,由正弦定理知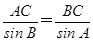 ,
,
从而sin Bcos A=3sin Acos B,
又因为0<A+B<π,所以cos A>0,cos B>0,所以tan B=3tan A.
(2)因为cos C=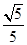 ,0<C<π,所以sin C=
,0<C<π,所以sin C=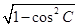 =
=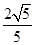 ,
,
从而tan C=2,于是tan[π-(A+B)]=2,即tan(A+B)=-2,
亦即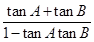 =-2,由(1)得
=-2,由(1)得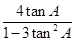 =-2,解得tan A=1或-
=-2,解得tan A=1或-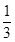 ,
,
因为cos A>0,故tan A=1,所以A=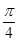 .
.
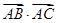 =3
=3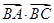 ,所以AB·AC·cos A=3BA·BC·cos B,
,所以AB·AC·cos A=3BA·BC·cos B,即AC·cos A=3BC·cos B,由正弦定理知
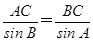 ,
,从而sin Bcos A=3sin Acos B,
又因为0<A+B<π,所以cos A>0,cos B>0,所以tan B=3tan A.
(2)因为cos C=
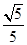 ,0<C<π,所以sin C=
,0<C<π,所以sin C=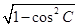 =
=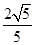 ,
,从而tan C=2,于是tan[π-(A+B)]=2,即tan(A+B)=-2,
亦即
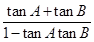 =-2,由(1)得
=-2,由(1)得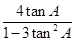 =-2,解得tan A=1或-
=-2,解得tan A=1或-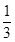 ,
,因为cos A>0,故tan A=1,所以A=
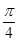 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
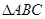 中,角
中,角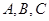 的对边分别为
的对边分别为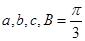 ,
,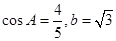 。
。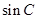 的值;
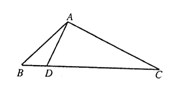
的值;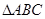 中,已知点
中,已知点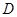 在
在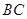 边上,满足
边上,满足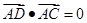 ,
,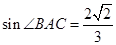 ,
,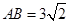 ,
,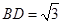 .
.
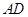 的长;
的长;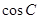 .
.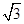 ,C=45°,则a=________.
,C=45°,则a=________.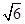 ,C=30°,则∠A=________.
,C=30°,则∠A=________.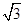 BD,BC=2BD,则sin C的值为________.
BD,BC=2BD,则sin C的值为________.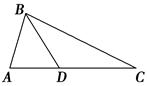
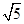 ,∠B=
,∠B=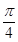 ,sin C=
,sin C= ,则c=________,a=________.
,则c=________,a=________.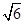 ,∠B=2∠A.
,∠B=2∠A.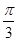 , sin B=3sin C.
, sin B=3sin C.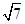 ,求△ABC的面积.
,求△ABC的面积.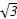 ,A=
,A=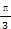 ,cosB=
,cosB=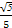 ,则b=( )
,则b=( )