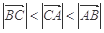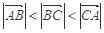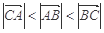题目内容
在△ABC中,角A,B,C的对边分别为a,b,c,已知角A=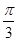 , sin B=3sin C.
, sin B=3sin C.
(1)求tan C的值;
(2)若a=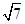 ,求△ABC的面积.
,求△ABC的面积.
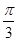 , sin B=3sin C.
, sin B=3sin C.(1)求tan C的值;
(2)若a=
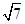 ,求△ABC的面积.
,求△ABC的面积.(1)  (2)
(2) 
 (2)
(2) 
(1)因为A=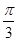 ,所以B+C=
,所以B+C= ,
,
故sin =3sin C,
=3sin C,
所以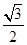 cos C+
cos C+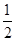 sin C=3sin C,即
sin C=3sin C,即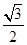 cos C=
cos C= sin C,得tan C=
sin C,得tan C= .
.
(2)由 ,sin B=3sin C,得b=3c.
,sin B=3sin C,得b=3c.
在△ABC中,由余弦定理,得a2=b2+c2-2bccos A=9c2+c2-2×(3c)×c×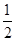 =7c2,
=7c2,
又∵a=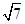 ,∴c=1,b=3,所以△ABC的面积为S=
,∴c=1,b=3,所以△ABC的面积为S=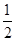 bcsin A=
bcsin A= .
.
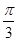 ,所以B+C=
,所以B+C= ,
,故sin
 =3sin C,
=3sin C,所以
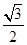 cos C+
cos C+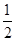 sin C=3sin C,即
sin C=3sin C,即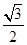 cos C=
cos C= sin C,得tan C=
sin C,得tan C= .
.(2)由
 ,sin B=3sin C,得b=3c.
,sin B=3sin C,得b=3c.在△ABC中,由余弦定理,得a2=b2+c2-2bccos A=9c2+c2-2×(3c)×c×
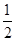 =7c2,
=7c2,又∵a=
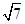 ,∴c=1,b=3,所以△ABC的面积为S=
,∴c=1,b=3,所以△ABC的面积为S=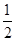 bcsin A=
bcsin A= .
.
练习册系列答案
相关题目
 .(1)求内角B的余弦值;(2)若
.(1)求内角B的余弦值;(2)若 ,求三角形
,求三角形 的面积.
的面积.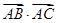 =3
=3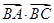 .
.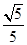 ,求A的值.
,求A的值.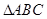 中,角
中,角 ,
, ,
, 对应的边分别是
对应的边分别是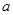 ,
,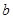 ,
,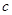 .已知
.已知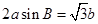 .
.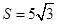 ,
,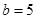 ,求
,求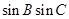 的值.
的值.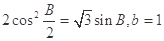 .
.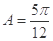 ,求边c的大小;
,求边c的大小; ,AB=
,AB=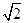 ,BC=3,则sin ∠BAC=( ).
,BC=3,则sin ∠BAC=( ).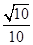
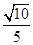
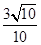
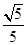
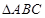 的内角
的内角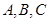 所对边的长分别为
所对边的长分别为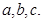 若
若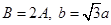 ,则角
,则角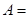 ( )
( )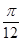
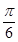
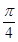
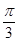
 的值为( ).
的值为( ).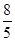
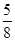
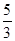
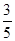
 三点不共线,且有
三点不共线,且有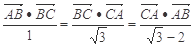 ,则有 ( )
,则有 ( )