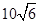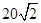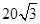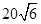题目内容
在△ABC中,a=3,b=2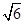 ,∠B=2∠A.
,∠B=2∠A.
(1)求cos A的值;
(2)求c的值.
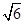 ,∠B=2∠A.
,∠B=2∠A.(1)求cos A的值;
(2)求c的值.
(1) (2)5
(2)5
 (2)5
(2)5(1)在△ABC中,由正弦定理
 ∴cos A=
∴cos A= .
.
(2)由余弦定理,a2=b2+c2-2bccos A⇒32=(2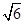 )2+c2-2×2
)2+c2-2×2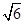 c×
c× ,
,
则c2-8c+15=0.∴c=5或c=3.
当c=3时,a=c,∴A=C.
由A+B+C=π,知B= ,与a2+c2≠b2矛盾.
,与a2+c2≠b2矛盾.
∴c=3舍去.故c的值为5.
 ∴cos A=
∴cos A= .
.(2)由余弦定理,a2=b2+c2-2bccos A⇒32=(2
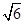 )2+c2-2×2
)2+c2-2×2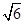 c×
c× ,
,则c2-8c+15=0.∴c=5或c=3.
当c=3时,a=c,∴A=C.
由A+B+C=π,知B=
 ,与a2+c2≠b2矛盾.
,与a2+c2≠b2矛盾.∴c=3舍去.故c的值为5.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
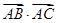 =3
=3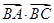 .
.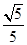 ,求A的值.
,求A的值.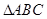 中,角
中,角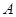 ,
,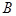 ,
,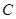 对应的边分别是
对应的边分别是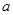 ,
,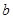 ,
,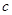 .已知
.已知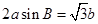 .
.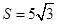 ,
,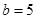 ,求
,求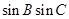 的值.
的值.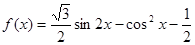 ,
,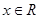
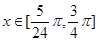 ,求函数
,求函数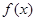 的最大值和最小值,并写出相应的x的值;
的最大值和最小值,并写出相应的x的值;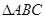 的内角
的内角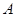 、
、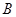 、
、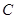 的对边分别为
的对边分别为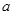 、
、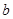 、
、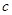 ,满足
,满足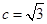 ,
,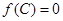 且
且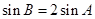 ,求
,求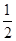 c=acosC,则A等于( )
c=acosC,则A等于( )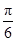 (B)
(B) 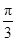
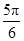 (D)
(D) 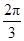
 cos B-sin(A-B)sin B+cos(A+C)=-
cos B-sin(A-B)sin B+cos(A+C)=- .
. ,b=5,求向量
,b=5,求向量 在
在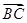 方向上的投影.
方向上的投影. ,AB=
,AB=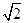 ,BC=3,则sin ∠BAC=( ).
,BC=3,则sin ∠BAC=( ).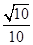
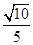
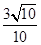
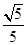
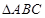 的内角
的内角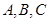 所对边的长分别为
所对边的长分别为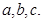 若
若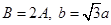 ,则角
,则角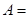 ( )
( )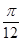
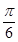
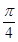
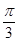
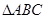 中,
中,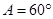 ,
,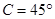 ,
,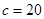 ,则边
,则边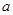 的长为( )
的长为( )