题目内容
【题目】设数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() .
.
(1)求出![]() ,
,![]() ,
,![]() 的值,并求出
的值,并求出![]() 及数列
及数列![]() 的通项公式;
的通项公式;
(2)设![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)设![]() ,在数列
,在数列![]() 中取出
中取出![]() (
(![]() 且
且![]() )项,按照原来的顺序排列成一列,构成等比数列
)项,按照原来的顺序排列成一列,构成等比数列![]() ,若对任意的数列
,若对任意的数列![]() ,均有
,均有![]() ,试求
,试求![]() 的最小值.
的最小值.
【答案】(1)![]() ,
,![]() ,
,![]() ,
,![]() .
.![]() ;(2)
;(2)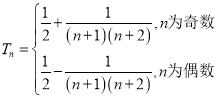 (3)2
(3)2
【解析】
(1)利用![]() 及
及![]() 整理可知
整理可知![]() ,通过计算出前三项的值,利用归纳推理猜想
,通过计算出前三项的值,利用归纳推理猜想![]() ,进而利用数学归纳法证明即可;
,进而利用数学归纳法证明即可;
(2)通过(1)裂项可知![]() ,进而分
,进而分![]() 为奇数、偶数两种情况讨论即可;
为奇数、偶数两种情况讨论即可;
(3)通过(1)可知![]() ,进而问题转化为求首项为1、公比为
,进而问题转化为求首项为1、公比为![]() 的等比数列的前
的等比数列的前![]() 项和.
项和.
解:(1)∵![]() ,
,
∴![]() ,即
,即![]() ,
,
又∵![]() ,即
,即![]() ,
,
∴ ,
, ,
,
…
猜想:![]() .
.
下面用数学归纳法来证明:
①当![]() 时,命题成立;
时,命题成立;
②假设当![]() 时,有
时,有![]() ,
,
则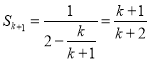 ,
,
即当![]() 时,命题也成立;
时,命题也成立;
由①②可知![]() .
.
∴![]() ,
,
又∵![]() 满足上式,
满足上式,
∴数列![]() 的通项公式
的通项公式![]() ;
;
(2)由(1)可知,![]() ,
,
特别地,当![]() 为奇数时,
为奇数时,![]() 为偶数,此时
为偶数,此时![]() ,
,
①若![]() 为偶数,则
为偶数,则![]()
![]()
![]()
![]() ;
;
②当![]() 为奇数且
为奇数且![]() 时,
时,![]() ,
,
故![]() ,
,
又∵![]() 满足上式,
满足上式,
∴当![]() 为奇数时,
为奇数时,![]() ;
;
由①②可知: ;
;
(3)由(1)可知![]() ,
,
∴![]() ,
,
由题意可知需等比数列![]() 的首项及公比均达到最大,显然首项为1公比为
的首项及公比均达到最大,显然首项为1公比为![]() ,
,
∴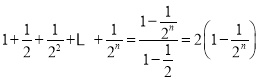 ,
,
∵![]() ,
,
∴![]() 的最小值为2.
的最小值为2.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目