题目内容
【题目】设![]() ,
,![]() .已知函数
.已知函数![]() ,
,![]() .
.
(Ⅰ)求![]() 的单调区间;
的单调区间;
(Ⅱ)已知函数![]() 和
和![]() 的图象在公共点(x0,y0)处有相同的切线,
的图象在公共点(x0,y0)处有相同的切线,
(i)求证:![]() 在
在![]() 处的导数等于0;
处的导数等于0;
(ii)若关于x的不等式![]() 在区间
在区间![]() 上恒成立,求b的取值范围.
上恒成立,求b的取值范围.
【答案】(I)单调递增区间为![]() ,
,![]() ,单调递减区间为
,单调递减区间为![]() .(II)(i)见解析.(ii)
.(II)(i)见解析.(ii)![]() .
.
【解析】
试题求导数后因式分解根据![]() ,得出
,得出![]() ,根据导数的符号判断函数的单调性,给出单调区间,对
,根据导数的符号判断函数的单调性,给出单调区间,对![]() 求导,根据函数
求导,根据函数![]() 和
和![]() 的图象在公共点(x0,y0)处有相同的切线,解得
的图象在公共点(x0,y0)处有相同的切线,解得![]() ,根据
,根据![]() 的单调性可知
的单调性可知![]() 在
在![]() 上恒成立,关于x的不等式
上恒成立,关于x的不等式![]() 在区间
在区间![]() 上恒成立,得出
上恒成立,得出![]() ,得
,得![]() ,
,![]() ,
,
求出![]() 的范围,得出
的范围,得出![]() 的范围.
的范围.
试题解析:(I)由![]() ,可得
,可得
![]() ,
,
令![]() ,解得
,解得![]() ,或
,或![]() .由
.由![]() ,得
,得![]() .
.
当![]() 变化时,
变化时,![]() ,
,![]() 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
|
|
|
|
所以,![]() 的单调递增区间为
的单调递增区间为![]() ,
,![]() ,单调递减区间为
,单调递减区间为![]() .
.
(II)(i)因为![]() ,由题意知
,由题意知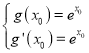 ,
,
所以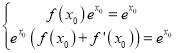 ,解得
,解得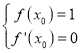 .
.
所以,![]() 在
在![]() 处的导数等于0.
处的导数等于0.
(ii)因为![]() ,
,![]() ,由
,由![]() ,可得
,可得![]() .
.
又因为![]() ,
,![]() ,故
,故![]() 为
为![]() 的极大值点,由(I)知
的极大值点,由(I)知![]() .
.
另一方面,由于![]() ,故
,故![]() ,
,
由(I)知![]() 在
在![]() 内单调递增,在
内单调递增,在![]() 内单调递减,
内单调递减,
故当![]() 时,
时,![]() 在
在![]() 上恒成立,从而
上恒成立,从而![]() 在
在![]() 上恒成立.
上恒成立.
由![]() ,得
,得![]() ,
,![]() .
.
令![]() ,
,![]() ,所以
,所以![]() ,
,
令![]() ,解得
,解得![]() (舍去),或
(舍去),或![]() .
.
因为![]() ,
,![]() ,
,![]() ,故
,故![]() 的值域为
的值域为![]() .
.
所以,![]() 的取值范围是
的取值范围是![]() .
.

 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案【题目】某保险公司利用简单随机抽样方法,对投保车辆进行抽样,样本车辆中每辆车的赔付结果统计如下:
赔付金额(元) | 0 | 1 000 | 2 000 | 3 000 | 4 000 |
车辆数(辆) | 500 | 130 | 100 | 150 | 120 |
(1)若每辆车的投保金额均为2800元,估计赔付金额大于投保金额的概率.
(2)在样本车辆中,车主是新司机的占10%,在赔付金额为4000元的样本车辆中,车主是新司机的占20%,估计在已投保车辆中,新司机获赔金额为4000元的概率.
【题目】某网站针对“2016年春节放假安排”开展网上问卷调查,提出了A,B两种放假方案,调查结果如表:(单位:万人)
人群 | 青少年 | 中年人 | 老年人 |
支持A方案 | 200 | 400 | 800 |
支持B方案 | 100 | 100 | n |
已知从所有参与调查的人中任选1人是“老年人”的概率为![]() .
.
(1)求n的值;
(2)从参与调查的“老年人”中,用分层抽样的方法抽取6人,在这6人中任意选取2人,求恰好有1人“支持B方案”的概率.