题目内容
【题目】已知椭圆![]() 的离心率
的离心率![]() ,过点
,过点![]() 的直线与原点的距离为
的直线与原点的距离为![]() .
.
(1)求椭圆方程;
(2)若直线![]() 与椭圆交于
与椭圆交于![]() 两点,试求
两点,试求![]() 面积的范围.
面积的范围.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1) 根据题意,求出直线![]() 的方程,再根据点到直线的距离公式,列出
的方程,再根据点到直线的距离公式,列出![]() 的等式关系,再结合离心率
的等式关系,再结合离心率![]() 以及
以及![]() 联立方程求解,即可求出椭圆方程.
联立方程求解,即可求出椭圆方程.
(2) 设出![]() 的坐标,将直线
的坐标,将直线![]() 与椭圆方程联立,得到联立方程,根据
与椭圆方程联立,得到联立方程,根据![]() 求出
求出![]() 的范围,再利用弦长公式表达出
的范围,再利用弦长公式表达出![]() 作为三角形的底,再求出原点到直线
作为三角形的底,再求出原点到直线![]() 的距离作为三角形的高,从而表达出三角形的面积关于
的距离作为三角形的高,从而表达出三角形的面积关于![]() 的函数,结合
的函数,结合![]() 的范围即可求出
的范围即可求出![]() 面积的范围.
面积的范围.
(1)由题意可知,直线AB的方程为![]() ,即
,即![]() ,
,
∵过点![]() 的直线与原点的距离为
的直线与原点的距离为![]() .
.
∴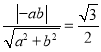 ,
,
∴由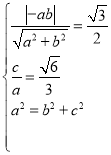 ,解得
,解得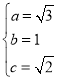 ,
,
∴椭圆方程为:![]() ;
;
(2)设点![]() ,
,
联立方程 ,消去
,消去![]() 得:
得:![]() ,
,
![]() ,解得
,解得![]()
![]() ,
,![]() ,
,
![]() ,
,
又∵原点到直线![]() 的距离
的距离![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴S△OPQ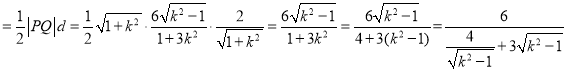
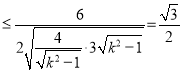 ,
,
∴![]() ,
,
∴![]() 面积的范围为
面积的范围为![]() .
.

 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案【题目】在2018、2019每高考数学全国Ⅰ卷中,第22题考查坐标系和参数方程,第23题考查不等式选讲.2018年髙考结束后,某校经统计发现:选择第22题的考生较多并且得分率也较高.为研究2019年选做题得分情况,该校高三质量检测的命题完全采用2019年高考选做题模式,在测试结束后,该校数学教师对全校高三学生的选做题得分进行抽样统计,得到两题得分的统计表如下(已知每名学生只选做—道题):
第22题的得分统计表
得分 | 0 | 3 | 5 | 8 | 10 |
理科人数 | 50 | 50 | 75 | 125 | 200 |
文科人数 | 25 | 25 | 125 | 0 | 25 |
第23题的得分统计表
得分 | 0 | 3 | 5 | 8 | 10 |
理科人数 | 30 | 52 | 58 | 60 | 200 |
文科人数 | 5 | 10 | 10 | 5 | 70 |
(1)完成如下2×2列联表,并判断能否有99%的把握认为“选做题的选择”与“文、理科的科类”有关;
选做22题 | 选做23题 | 总计 | |
理科人数 | |||
文科人数 | |||
总计 |
(2)若以全体高三学生选题的平均得分作为决策依据,如果你是考生,根据上面统计数据,你会选做哪道题,并说明理由.
附:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |