题目内容
【题目】设![]() 分别是椭圈
分别是椭圈![]() 的左、右焦点,
的左、右焦点,![]() 是椭圆上第二象限内的一点且
是椭圆上第二象限内的一点且![]() 与
与![]() 轴垂直,直线
轴垂直,直线![]() 与椭圆的另一个交点为
与椭圆的另一个交点为![]() .
.
(1)若直线![]() 的斜率为
的斜率为![]() ,求椭圆的离心率;
,求椭圆的离心率;
(2)若直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,且
,且![]() 求
求![]() .
.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1) 根据题意,先求出点![]() 的坐标,再表达出直线
的坐标,再表达出直线![]() 的斜率,再根据椭圆的性质
的斜率,再根据椭圆的性质![]() ,从而得到
,从而得到![]() 的等量关系,从而求出椭圆的离心率.
的等量关系,从而求出椭圆的离心率.
(2) 根据直线![]() 与
与![]() 轴的交点为
轴的交点为![]() 且点
且点![]() 为
为![]() 的中点求出
的中点求出![]() ,再根据
,再根据![]() ,建立方程组关系,求出点
,建立方程组关系,求出点![]() 的坐标,代入椭圆方程即可得出结果.
的坐标,代入椭圆方程即可得出结果.
(1)由题意可知点![]() 的横坐标为
的横坐标为![]() ,代入椭圆方程得:
,代入椭圆方程得:![]() ,解得
,解得![]() ,
,
![]() 点
点 ,又
,又![]() 点
点![]() ,
,
∴直线![]() 的斜率为
的斜率为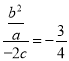 ,即
,即![]() ,
,
又![]() ,
, ![]() ,
,
两边同时除以![]() 得:
得:![]() ,解得
,解得![]() ,
,
∴椭圆的离心率为![]() ;
;
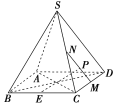
(2)如图所示:

![]() 原点O是
原点O是![]() 的中点,
的中点,![]() ,
,![]() 点D为
点D为![]() 的中点,又点
的中点,又点 ,点
,点![]() ,
,
![]() ,
,![]() ,
,
设点![]() ,
, ![]() ,
,![]() ,
,![]() ,
,
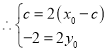 ,
,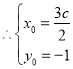 ,
,![]() 点
点![]() ,
,
把点![]() 坐标代入椭圆方程得:
坐标代入椭圆方程得:![]() ,
,
![]() 由
由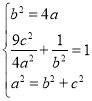 ,解得
,解得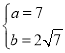 ,
,
![]() .
.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目