题目内容
【题目】在一次跳绳活动中,某学校从高二年级抽取了100位同学一分钟内跳绳,由测量结果得到如图所示的频率分布直方图,落在区间[140,150),[150,160),[160,170]内的频率之比为4:2:1.
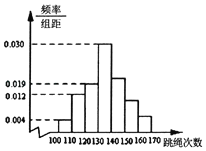
(1)求跳绳次数落在区间[150,160)内的频率;
(2)用分层抽样的方法在区间[130,160)内抽取6位同学,将该样本看成一个总体,从中任意抽取2位同学,求这2位同学跳绳次数都在区间[130,150)内的概率.
【答案】(1)0.10;(2)![]()
【解析】
(1)由图中小矩形的面积之和为1可得[140,170)的频率,再由频率之比即得;(2)先确定[140,150),[150,160),[160,170]三个区间的频率,再分层抽样,最后根据古典概型求出概率。
(1)∵图中小矩形的面积之和为1,
∴[140,170)的频率为:1﹣(0.04+0.12+0.19+0.30)=0.35,
∵[140,150),[150,160),[160,170)的频率之比为4:2:1,
∴[150,160)的频率为![]() 0.10,
0.10,
(2)∵区间[140,150)的频率为![]() 0.20,
0.20,
∴[130,140),[140,150),[150,160)内的频率依次为0.30,0.20,0.10,
用分层抽样的方法在区间[130,160)内抽取一个容量为6的样本,
则在区间[130,140)内应抽取6![]() 3,设为A1,A2,A3,
3,设为A1,A2,A3,
在区间[140,150)内应抽取6![]() 2,记为B1,B2,
2,记为B1,B2,
在区间[150,160)内应抽取6![]() 1,记为C,
1,记为C,
设“从样本中任意抽取2位同学,这2位同学都在区间[130,150)内”这事件M,
则所有的基本事件有15个,分别为:
(A1,A2),(A1,A3),(A1,B1),(A1,B2),(A1,C),(A2,A3),(A2,B1),(A2,B2),
(A2,C),(A3,B1),(A3,B2),(A3,C),(B1,B2),(B1,C),(B2,C),
事件M包含的基本事件有10种,分别为:
(A1,A2),(A1,A3),(A1,B1),(A1,B2),(A2,A3),(A2,B1),(A2,B2),(A3,B1),(A3,B2),(B1,B2),
∴这2位同学跳绳次数都在区间[130,150)内的概率P(M)![]() .
.

 名师点拨卷系列答案
名师点拨卷系列答案【题目】某学校高三年级有学生500人,其中男生300人,女生200人,为了研究学生的数学成绩是否与性别有关,现采用分层抽样的方法,从中抽取了100名学生,先统计了他们期中考试的数学分数,然后按性别分为男、女两组,再将两组学生的分数分成5组:[100,110),[110,120),[120,130),[130,140),[140,150]分别加以统计,得到如图所示的频率分布直方图.
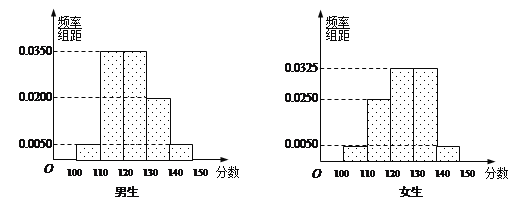
(1)从样本中分数小于110分的学生中随机抽取2人,求两人恰好为一男一女的概率;
(2)若规定分数不小于130分的学生为“数学尖子生”,请你根据已知条件完成2×2列联表,并判断是否有90%的把握认为“数学尖子生与性别有关”?
附:
P(K2≥k0) | 0.100 | 0.050 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 6.635 | 10.828 |
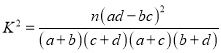 ,
,