题目内容
【题目】在平面直角坐标系中,O是坐标原点,两定点A,B满足| ![]() |=|
|=| ![]() |=
|= ![]()
![]() =2,则点集{P|
=2,则点集{P| ![]() =λ
=λ ![]() +μ
+μ ![]() ,|λ|+|μ|≤1,λ,μ∈R}所表示的区域的面积是( )
,|λ|+|μ|≤1,λ,μ∈R}所表示的区域的面积是( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】D
【解析】解:由两定点A,B满足 ![]() =
= ![]() =2,
=2, ![]() =
= ![]() ﹣
﹣ ![]() ,则|
,则| ![]() |2=(
|2=( ![]() ﹣
﹣ ![]() )2=
)2= ![]() ﹣2
﹣2 ![]()
![]() +
+ ![]() =4,则|
=4,则| ![]() |=2,说明O,A,B三点构成边长为2的等边三角形.
|=2,说明O,A,B三点构成边长为2的等边三角形.
不妨设A( ![]() ),B(
),B( ![]() ).再设P(x,y).
).再设P(x,y).
由 ![]() ,得:
,得: ![]() .
.
所以 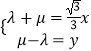 ,解得
,解得 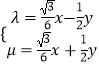 ①.
①.
由|λ|+|μ|≤1.
所以①等价于 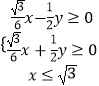 或
或 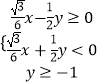 或
或 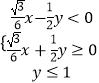 或
或 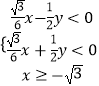 .
.
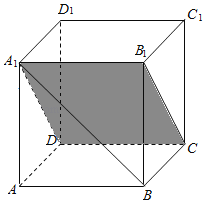
可行域如图中矩形ABCD及其内部区域,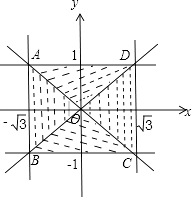
则区域面积为 ![]() .
.
故选D.
【考点精析】通过灵活运用二元一次不等式(组)所表示的平面区域和平面向量的基本定理及其意义,掌握不等式组表示的平面区域是各个不等式所表示的平面区域的公共部;如果![]() 、
、![]() 是同一平面内的两个不共线向量,那么对于这一平面内的任意向量
是同一平面内的两个不共线向量,那么对于这一平面内的任意向量![]() ,有且只有一对实数
,有且只有一对实数![]() 、
、![]() ,使
,使![]() 即可以解答此题.
即可以解答此题.

 优学名师名题系列答案
优学名师名题系列答案【题目】随着支付宝、微信等支付方式的上线,越来越多的商业场景可以实现手机支付.有关部门为了了解各年龄段的人使用手机支付的情况,随机调查了50次商业行为,并把调查结果制成下表:
年龄(岁) |
|
|
|
|
|
|
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
手机支付 | 4 | 6 | 10 | 6 | 2 | 0 |
(1)若把年龄在![]() 的人称为中青年,年龄在
的人称为中青年,年龄在![]() 的人称为中老年,请根据上表完成以下
的人称为中老年,请根据上表完成以下![]() 列联表;并判断是否可以在犯错误的概率不超过0.05的前提下,认为使用手机支付与年龄(中青年、中老年)有关系?
列联表;并判断是否可以在犯错误的概率不超过0.05的前提下,认为使用手机支付与年龄(中青年、中老年)有关系?
手机支付 | 未使用手机支付 | 总计 | |
中青年 | |||
中老年 | |||
总计 |
(2)若从年龄在![]() 的被调查中随机选取2人进行调查,记选中的2人中,使用手机支付的人数为
的被调查中随机选取2人进行调查,记选中的2人中,使用手机支付的人数为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
参考公式:![]() ,其中
,其中![]() .
.
独立性检验临界值表:
| 0.15 | 0.10 | 0.005 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
【题目】某学校高三年级学生某次身体素质体能测试的原始成绩采用百分制,已知所有这些学生的原始成绩均分布在![]() 内,发布成绩使用等级制,各等级划分标准见下表.
内,发布成绩使用等级制,各等级划分标准见下表.
百分制 | 85分及以上 | 70分到84分 | 60分到69分 | 60分以下 |
等级 | A | B | C | D |
规定:A,B,C三级为合格等级,D为不合格等级为了解该校高三年级学生身体素质情况,从中抽取了n名学生的原始成绩作为样本进行统计.
按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的分组作出频率分布直方图如图1所示,样本中分数在80分及以上的所有数据的茎叶图如图2所示
的分组作出频率分布直方图如图1所示,样本中分数在80分及以上的所有数据的茎叶图如图2所示
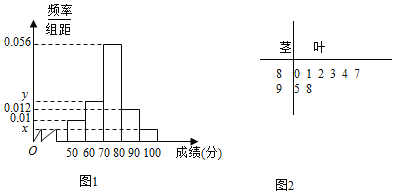
![]() 求n和频率分布直方图中的x,y的值,并估计该校高一年级学生成绩是合格等级的概率;
求n和频率分布直方图中的x,y的值,并估计该校高一年级学生成绩是合格等级的概率;
![]() 根据频率分布直方图,求成绩的中位数
根据频率分布直方图,求成绩的中位数![]() 精确到
精确到![]() ;
;
![]() 在选取的样本中,从A,D两个等级的学生中随机抽取2名学生进行调研,求至少有一名学生是A等级的概率.
在选取的样本中,从A,D两个等级的学生中随机抽取2名学生进行调研,求至少有一名学生是A等级的概率.