Question

【题目】设函数fn（x）=﹣1+x+ + +…+ （x∈R，n∈N+），证明：
（1）对每个n∈N+ ， 存在唯一的x∈[ ，1]，满足fn（xn）=0；
（2）对于任意p∈N+ ， 由（1）中xn构成数列{xn}满足0＜xn﹣xn+p＜ ．

Answer 1

【答案】
（1）证明：对每个n∈N+，当x＞0时，由函数fn（x）=﹣1+x+ ），可得

f′（x）=1+ + +… ＞0，故函数f（x）在（0，+∞）上是增函数．

由于f1（x1）=0，当n≥2时，fn（1）= + +…+ ＞0，即fn（1）＞0．

又fn（ ）=﹣1+ +[ + + +…+ ]≤﹣ +

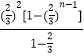=﹣ + × =﹣ ＜0，

根据函数的零点的判定定理，可得存在唯一的xn ，满足fn（xn）=0

（2）证明：对于任意p∈N+，由（1）中xn构成数列{xn}，当x＞0时，∵fn+1（x）=fn（x）+ ＞fn（x），

∴fn+1（xn）＞fn（xn）=fn+1（xn+1）=0．

由 fn+1（x） 在（0，+∞）上单调递增，可得 xn+1＜xn，即 xn﹣xn+1＞0，故数列{xn}为减数列，即对任意的 n、p∈N+，xn﹣x/span>n+p＞0．

由于 fn（xn）=﹣1+xn+ + +…+ =0 ①，

fn+p （xn+p）=﹣1+xn+p+ + +…+ +[ + +…+ ]②，

用①减去②并移项，利用 0＜xn+p≤1，可得

xn﹣xn+p= + ≤ ≤ ＜ = ＜ ．

综上可得，对于任意p∈N+，由（1）中xn构成数列{xn}满足0＜xn﹣xn+p＜

【解析】（1）由题意可得f′（x）＞0，函数f（x）在（0，+∞）上是增函数．求得fn（1）＞0，fn（ ）＜0，再根据函数的零点的判定定理，可得要证的结论成立．（2）由题意可得fn+1（xn）＞fn（xn）=fn+1（xn+1）=0，由 fn+1（x） 在（0，+∞）上单调递增，可得 xn+1＜xn ， 故xn﹣xn+p＞0．用 fn（x）的解析式减去fn+p （xn+p）的解析式，变形可得xn﹣xn+p= + ，再进行放大，并裂项求和，可得它小于 ，综上可得要证的结论成立．
【考点精析】本题主要考查了基本求导法则和数列的前n项和的相关知识点，需要掌握若两个函数可导，则它们和、差、积、商必可导；若两个函数均不可导，则它们的和、差、积、商不一定不可导；数列{an}的前n项和sn与通项an的关系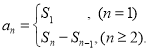才能正确解答此题．