��Ŀ����
����Ŀ���ҹ�������������ȱˮ�Ĺ���֮һ������ȱˮ�����Ϊͻ����ij��Ϊ�˽�Լ������ˮ���ƻ��ڱ������о���������ˮ�����������ȷ��һ�������¾���ˮ������ˮ��������a�IJ��ְ���ƽ���շѣ�����a�IJ��ְ�������շѣ���Ϊ�˽�Ϊ������ȷ�����������ͨ����������� 100λ����ij����¾���ˮ������λ��t����������Ƶ�ʷֲ�ֱ��ͼ�� 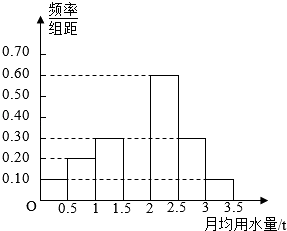
��1������ij��ԭ��Ƶ�ʷֲ�ֱ��ͼ�������ݶ�ʧ������ͼ�н��䲹��������
��2���������������壬���ϣ��80%�ľ���ÿ�µ���ˮ�������������¾���ˮ������ͱ���Ϊ���ٶ֣���˵�����ɣ�
��3����Ƶ�ʷֲ�ֱ��ͼ�й��Ƹ�100λ�����¾���ˮ������������λ����ƽ������ͬһ���е������ø�������е�ֵ��������
���𰸡�
��1���⣺��������ã�1.5��2t���û��� ![]() =0.4����ͼ��ʾ��
=0.4����ͼ��ʾ��
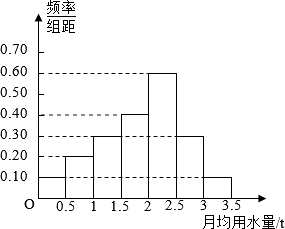
��2���⣺�¾���ˮ������ͱ�Ӧ��Ϊ2.5�֣�����Ϊ��
�������¾���ˮ��������2.5�ֵľ�����20λ��ռ���������20%��
�������������壬Ҫ��֤80%�ľ���ÿ�µ���ˮ�������������¾���ˮ������ͱ�Ӧ��Ϊ2.5��
��3���⣺��100λ������¾���ˮ��������2.25����λ��2��
ƽ����Ϊ0.5���� ![]() ��0.10+
��0.10+ ![]() ��0.20+
��0.20+ ![]() ��0.30+
��0.30+ ![]() ��0.40+
��0.40+ ![]() ��0.60+
��0.60+ ![]() ��0.30+
��0.30+ ![]() ��0.10��=1.875
��0.10��=1.875
����������1����������ȷ����1.5��2t�û��� ![]() ����ȫƵ�ʷֲ�ֱ��ͼ���ɣ���2���¾���ˮ������ͱ�Ӧ��Ϊ2.5�֣�����Ϊ���������¾���ˮ��������2.5�ֵľ�����20λ��ռ���������20%�������������������������ͼ��ɣ���3���ҳ�������ˮ������������λ�������ƽ�������ɣ�
����ȫƵ�ʷֲ�ֱ��ͼ���ɣ���2���¾���ˮ������ͱ�Ӧ��Ϊ2.5�֣�����Ϊ���������¾���ˮ��������2.5�ֵľ�����20λ��ռ���������20%�������������������������ͼ��ɣ���3���ҳ�������ˮ������������λ�������ƽ�������ɣ�