题目内容
【题目】一家面包房根据以往某种面包的销售记录,绘制了日销售量的频率分布直方图,如图所示.将日销售量落入各组的频率视为概率. 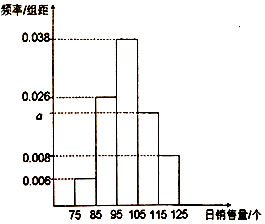
(1)求a的值并估计在一个月(按30天算)内日销售量不低于105个的天数;
(2)利用频率分布直方图估计每天销售量的平均值及方差(同一组中的数据用该组区间的中点值作代表).
【答案】
(1)解:(0.006+0.008+a+0.026+0.038)×10=1,
解得a=0.022;
日销售量不低于105个的概率为
P=(0.022+0.008)×10=0.3,
30×0.3=9,
故一个月内日销售量不低于105个的天数大约为9天
(2)解:日平均销售量的平均数为
![]() =80×0.06+90×0.26+100×0.38+110×0.22+120×0.08=100.
=80×0.06+90×0.26+100×0.38+110×0.22+120×0.08=100.
日平均销售量的方差为
s2=(﹣20)2×0.06+(﹣10)2×0.25+102×0.22+202×0.08=104,
日销售量的平均数的估计值为100,方差的估计值为104
【解析】(1)根据频率和为1,列出方程求出a的值,再根据频率、频数与样本容量的关系求出结果;(2)根据平均数与方差的定义进行计算即可.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目