题目内容
选修4—4:坐标系与参数方程
已知直线l的参数方程为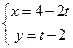 (t为参数),
(t为参数),
P是椭圆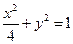 上任意一点,求点P到直线l距离的最大值.
上任意一点,求点P到直线l距离的最大值.
已知直线l的参数方程为
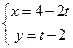 (t为参数),
(t为参数),P是椭圆
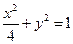 上任意一点,求点P到直线l距离的最大值.
上任意一点,求点P到直线l距离的最大值.解:直线l的参数方程为(t为参数),故直线l的普通方程为x+2y=0.…2分
因为P是椭圆+y2=1上任意一点,故可设P(2cosq,sinq)其中q∈R.………4分
因此点P到直线l的距离是d==. ………8分
所以当q=kp+,k∈Z时,d取得最大值. …………………………………10分
因为P是椭圆+y2=1上任意一点,故可设P(2cosq,sinq)其中q∈R.………4分
因此点P到直线l的距离是d==. ………8分
所以当q=kp+,k∈Z时,d取得最大值. …………………………………10分
略

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
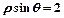 上,点Q在曲线
上,点Q在曲线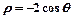 上,求|
上,求|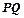 |的最小值.
|的最小值.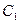 :
: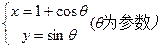 上求一点,使它到直线
上求一点,使它到直线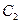 :
: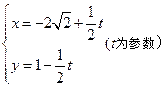 的距离最小,并求出该点坐标和最小距离。
的距离最小,并求出该点坐标和最小距离。 (参数t∈R),圆C的参数方程为
(参数t∈R),圆C的参数方程为 (参数
(参数 ),则圆C的圆心坐标为_______,圆心到直线l的距离为______.
),则圆C的圆心坐标为_______,圆心到直线l的距离为______.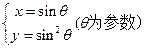 与直线
与直线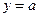 有两个公共点,则实数
有两个公共点,则实数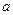 的取值范围是_________________.
的取值范围是_________________.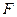 是曲线
是曲线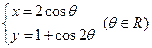 的焦点,
的焦点,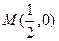 ,则
,则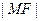 的值是 .
的值是 .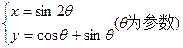 上的点是 ( )
上的点是 ( )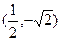
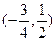
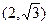
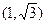
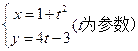 与
与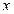 轴交点的直角坐标是( )
轴交点的直角坐标是( )


