题目内容
(选修4—4:坐标系与参数方程)
设点P在曲线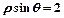 上,点Q在曲线
上,点Q在曲线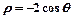 上,求|
上,求|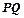 |的最小值.
|的最小值.
设点P在曲线
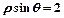 上,点Q在曲线
上,点Q在曲线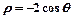 上,求|
上,求|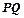 |的最小值.
|的最小值.|PQ|的最小值为2-1=1
解:以极点为原点,极轴所在直线为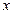 轴建立直角坐标系.
轴建立直角坐标系.
将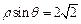 化为直角坐标方程,得直线方程
化为直角坐标方程,得直线方程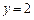 …………………………3分
…………………………3分
将 化为直角坐标方程,得圆方程
化为直角坐标方程,得圆方程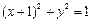 ………………………6分
………………………6分
所以圆心(-1,0)到直线距离为2,|PQ|的最小值为2-1=1……………………10分
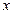 轴建立直角坐标系.
轴建立直角坐标系.将
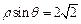 化为直角坐标方程,得直线方程
化为直角坐标方程,得直线方程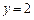 …………………………3分
…………………………3分将
 化为直角坐标方程,得圆方程
化为直角坐标方程,得圆方程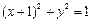 ………………………6分
………………………6分所以圆心(-1,0)到直线距离为2,|PQ|的最小值为2-1=1……………………10分

练习册系列答案
相关题目
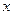 轴的正半轴重合,曲线
轴的正半轴重合,曲线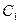 :
: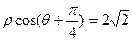 与曲线
与曲线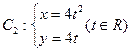 交于A、B两点。
交于A、B两点。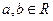 ,若
,若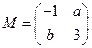 所对应的变换
所对应的变换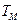 把直线
把直线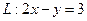 变换为自身,求实数
变换为自身,求实数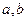 ,并求
,并求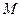 的逆矩阵。
的逆矩阵。 的参数方程:
的参数方程: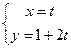 (
(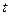 为参数)和圆
为参数)和圆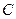 的极坐标方程:
的极坐标方程: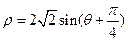 。
。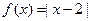
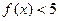 ;
;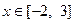 ,不等式
,不等式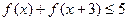 成立.
成立.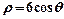 ,曲线C2的极坐标方程为
,曲线C2的极坐标方程为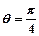 (
(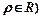 ,曲线C1,C2相交于点A,B。
,曲线C1,C2相交于点A,B。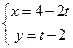 (t为参数),
(t为参数),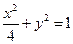 上任意一点,求点P到直线l距离的最大值.
上任意一点,求点P到直线l距离的最大值. 一题评阅记分)
一题评阅记分)
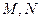 分别是曲线
分别是曲线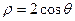 和
和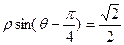 上的动点,则
上的动点,则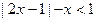 的解集是 ;
的解集是 ; 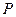 作圆
作圆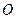 的割线
的割线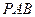 与切线
与切线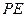 ,
,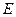 为切点,连接
为切点,连接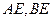 ,
,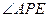 的平分线与
的平分线与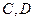 ,若
,若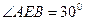 ,则
,则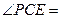 ;
;  为曲线
为曲线 的切线,且与直线
的切线,且与直线
 垂直.
垂直. 由直线
由直线 、
、 和
和 轴所围成的三角形
轴所围成的三角形 的面积.
的面积.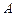 在曲线
在曲线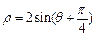 上,点
上,点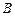 在直线
在直线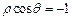 上,则
上,则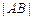 的最小值是 ** .
的最小值是 ** .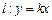 与曲线
与曲线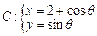 (参数
(参数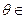 R)有唯一的公共点,则实数
R)有唯一的公共点,则实数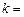 .
.