题目内容
【题目】一条直线上依次有三点![]() 、
、![]() 、
、![]() .一只猎犬在点
.一只猎犬在点![]() 发现一大两小三只兔子从点
发现一大两小三只兔子从点![]() 向兔穴(点
向兔穴(点![]() )前行,立即向它们追去.当兔子发现猎犬追赶后,急忙向兔穴奔跑,大兔为了提高速度,可叼着一只小兔奔跑(速度不变,且叼起与放下小兔所耽误的时间不计).已知
)前行,立即向它们追去.当兔子发现猎犬追赶后,急忙向兔穴奔跑,大兔为了提高速度,可叼着一只小兔奔跑(速度不变,且叼起与放下小兔所耽误的时间不计).已知![]() ,
,![]() ,猎犬、大兔、小兔奔跑的速度分别为
,猎犬、大兔、小兔奔跑的速度分别为![]() 、
、![]() 、
、![]() ,兔子前行的速度为
,兔子前行的速度为![]() .则三只兔子至多在离开点
.则三只兔子至多在离开点![]() ______
______![]() 时发现猎犬,才能恰在猎犬追上自己之前全部跑进兔穴.
时发现猎犬,才能恰在猎犬追上自己之前全部跑进兔穴.
【答案】![]()
【解析】
显然,猎犬跑到兔穴需要用![]() .
.
设兔子在离开点![]() 处
处![]() 时发现猎犬,此时已用时
时发现猎犬,此时已用时![]() .则剩下的
.则剩下的![]() 的路程,大兔需设法带领小兔在
的路程,大兔需设法带领小兔在![]() 内跑完.下面求
内跑完.下面求![]() .
.
考虑长为![]() 的路程
的路程![]() .
.
设三只兔子至少需![]() 跑完.大兔必须先叼一只小兔跑到前面的点
跑完.大兔必须先叼一只小兔跑到前面的点![]() ,放下小兔后,让这只小兔自己继续向前跑,大兔则向后跑去接另一只小兔,当与另一只小兔在点
,放下小兔后,让这只小兔自己继续向前跑,大兔则向后跑去接另一只小兔,当与另一只小兔在点![]() 相遇后,再叼起它向前跑,最终与前一只小兔同时到达点
相遇后,再叼起它向前跑,最终与前一只小兔同时到达点![]() .
.
因大、小兔的奔跑速度之比为3:2,故应将全程分成三段,比例为![]() .
.
所以,![]() .
.
易知,将全程分成若干段,在每段路程内都按上述方法奔跑与全程都按上述方法奔跑所用时间一样.从而,![]()
![]() .
.
故答案为:![]()

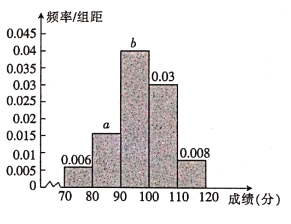
【题目】为迎接2022年北京冬季奥运会,普及冬奥知识,某校开展了“冰雪答题王”冬奥知识竞赛活动.现从参加冬奥知识竞赛活动的学生中随机抽取了100名学生,将他们的比赛成绩(满分为100分)分为6组:![]() ,
,![]() 得到如图所示的频率分布直方图.
得到如图所示的频率分布直方图.
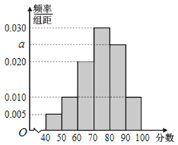
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)记![]() 表示事件“从参加冬奥知识竞赛活动的学生中随机抽取一名学生,该学生的比赛成绩不低于80分”,估计
表示事件“从参加冬奥知识竞赛活动的学生中随机抽取一名学生,该学生的比赛成绩不低于80分”,估计![]() 的概率;
的概率;
(Ⅲ)在抽取的100名学生中,规定:比赛成绩不低于80分为“优秀”,比赛成绩低于80分为“非优秀”.请在答题卡上将![]() 列联表补充完整,并判断是否有
列联表补充完整,并判断是否有![]() 的把握认为“比赛成绩是否优秀与性别有关”?
的把握认为“比赛成绩是否优秀与性别有关”?
参考公式及数据: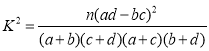 ,
,![]() .
.
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |