题目内容
【题目】2018年8月18日，举世瞩目的第18届亚运会在印尼首都雅加达举行，为了丰富亚运会志愿者的业余生活，同时鼓励更多的有志青年加入志愿者行列，大会主办方决定对150名志愿者组织一次有关体育运动的知识竞赛（满分120分）并计划对成绩前15名的志愿者进行奖励，现将所有志愿者的竞赛成绩制成频率分布直方图，如图所示，若第三组与第五组的频数之和是第二组的频数的3倍，试回答以下问题：
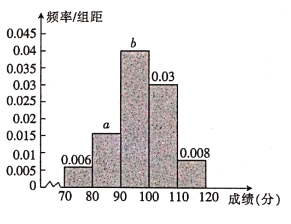
（1）求图中
的值；
（2）求志愿者知识竞赛的平均成绩；
（3）从受奖励的15人中按成绩利用分层抽样抽取5人，再从抽取的5人中，随机抽取2人在主会场服务，求抽取的这2人中其中一人成绩在
分的概率.
【答案】（1）
（2）96.8（3）
【解析】
(1)由频率分布直方图的性质结合条件即可求解；
(2)每个小长方形底边中点所对应的横坐标乘以该组的频率，再求和即可求出平均数；
(3)用列举法先求出从抽取的5人中，随机抽取2人所包含的基本事件总数，以及抽取的这2人中其中一人成绩在
分所包含的基本事件个数，结合古典概型的概率公式即可求出概率.
（1）由条件及频率分别直方图的性质可知：
解得
（2）由（1）可知，成绩在
分的有9人，在
分的有24人，
在
分的有60人，在分的有45人，
在
分的有12人，故志愿者知识竞赛平均成绩为
（3）由（2）可知，受奖励的15人中有三人的成绩是分，其余12人的成绩是分，利用分层抽样抽取5人，有1人成绩在分中，4人成绩在分中.
记成绩是分的1人为
，成绩是分的4人为
，从这5人中抽取2人去主会场服务共有以下10种可能：
，
，
，
，
，
，
，
，
，
，
满足条件的有，，，，共4种，
故所求概率
.
【题目】如图，在正方体
中，点
，
分别为棱
，
的中点，点
为上底面的中心，过，，三点的平面把正方体分为两部分，其中含
的部分为
，不含的部分为
，连结和的任一点
，设
与平面
所成角为
，则
的最大值为
A. 
B. 
C. 
D. 
【题目】通过市场调查,得到某种产品的资金投入x(单位:万元)与获得的利润y(单位:万元)的数据,如表所示:
资金投入x | 2 | 3 | 4 | 5 | 6 |
利润y | 2 | 3 | 5 | 6 | 9 |
(1)画出数据对应的散点图;
(2)根据上表提供的数据,用最小二乘法求线性回归直线方程
;
(3)现投入资金10万元,求获得利润的估计值为多少万元?
参考公式：