题目内容
【题目】在用1,2,…,8这八个数码所组成的 全部无重复数字的八位数中,能被11整除的有______个.
【答案】4608
【解析】
由于1,2,…,8中有4个奇数,故任意添加 “+”、“-”号后其代数和皆为偶数.因1,2,…,8中最大的四数和与最小的四数和之差不大于16,于是,符合条件的每个八位数,其奇数数位上的四个数码之和必等于偶数数位上的四个数码之和.由于
,再将1,2,…,8分成和为18的两组,每组四个数,并考虑含8的组,该组另三数的和为10,只有四种情况: (1,2,7,8),(1,3,6,8),(1,4,5,8),(2,3,5,8).
对于每种情况,可将含8的组排在奇数数位上或者偶数数位上,得到2×4!×4!个数.
四种情况下共得
个符合条件的八位数.
故答案为：4608
【题目】金秋九月，丹桂飘香，某高校迎来了一大批优秀的学生．新生接待其实也是和社会沟通的一个平台．校团委、学生会从在校学生中随机抽取了160名学生，对是否愿意投入到新生接待工作进行了问卷调查，统计数据如下：
愿意 | 不愿意 | |
男生 | 60 | 20 |
女士 | 40 | 40 |
（1）根据上表说明，能否有99%把握认为愿意参加新生接待工作与性别有关；
（2）现从参与问卷调查且愿意参加新生接待工作的学生中，采用按性别分层抽样的方法，选取5人．若从这5人中随机选取3人到火车站迎接新生，求选取的3人中恰好有1名女生的概率.
附：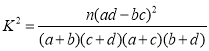
，其中
．
| 0.05 | 0.01 | 0.001 |
| 3.841 | 6.635 | 10.828 |
【题目】为了研究“教学方式”对教学质量的影响，某高中老师分别用两种不同的教学方式对入学数学平均分数和优秀率都相同的甲、乙两个高一新班进行教学（勤奋程度和自觉性都一样）．以下茎叶图为甲、乙两班(每班均为20人)学生的数学期末考试成绩．
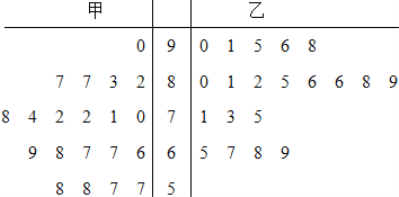
（1）现从甲班数学成绩不低于80分的同学中随机抽取两名同学，求成绩为87分的同学至少有一名被抽中的概率；
（2）学校规定：成绩不低于75分的为优秀．请填写下面的2×2列联表，并判断有多大把握认为“成绩优秀与教学方式有关”．
甲班 | 乙班 | 合计 | |
优秀 | |||
不优秀 | |||
合计 |
参考公式：
，其中
参考数据：
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
