题目内容
【题目】已知函数![]() .
.
(Ⅰ)若x轴为曲线![]() 的切线,求a的值;
的切线,求a的值;
(Ⅱ)求函数![]() 在
在![]() 上的最大值和最小值.
上的最大值和最小值.
【答案】(Ⅰ)![]() (Ⅱ)详见解析
(Ⅱ)详见解析
【解析】
(Ⅰ)求出函数的导数,设切点坐标为(x0,0),求出切线的斜率,转化求解即可;
(Ⅱ)求出f′(x)=3x2﹣a,通过当a≤0时,当a≥3时,当0<a<3时,判断导函数的符号,判断函数的单调性即可得到函数的最值.
解:(Ⅰ)由于x轴为![]() 的切线,设切点坐标为
的切线,设切点坐标为![]() ,则
,则![]() ,……①又
,……①又![]() ,即
,即![]() ,……②②代入①,解得
,……②②代入①,解得![]() ,
,
所以![]() .
.
(Ⅱ)![]() ,
,
(1)当![]() 时,
时,![]() ,
,![]() 在
在![]() 单调递增,所以
单调递增,所以![]() 时,
时,![]() 取得最小值
取得最小值![]() .
.
![]() 时,
时,![]() 取得最大值
取得最大值![]() .
.
(2)当![]() 时,
时,![]() ,
,![]() 在
在![]() 单调递减,所以,
单调递减,所以,![]() 时,
时,![]() 取得最小值
取得最小值![]() .
.
![]() 时,
时,![]() 取得最大值
取得最大值![]() .
.
(3).当![]() 时,令
时,令![]() ,解得
,解得![]() ,
,![]() ,
,![]() ,
,![]() 在区间
在区间![]() 的变化情况如下:
的变化情况如下:
|
|
|
|
|
| 0 |
|
| 单调递减↗ | 极小值 | 单调递增↘ |
由上表可知,当![]() 时,
时,![]() 取得最小值
取得最小值![]() ;
;
由于![]() ,
,![]() ,
,
当![]() 时,
时,![]() 在
在![]() 处取得最大值
处取得最大值![]() ,
,
当![]() 时,
时,![]() 在
在![]() 处取得最大值
处取得最大值![]() .
.

 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案【题目】为了研究“教学方式”对教学质量的影响,某高中数学老师分别用两种不同的教学方式对入学数学平均分数和优秀率都相同的甲、乙两个高一新班进行教学(勤奋程度和自觉性都一样).以下茎叶图为甲、乙两班(每班均为20人)学生的数学期末考试成绩.
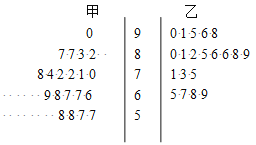
(1)学校规定:成绩不低于75分的为优秀.请画出下面的![]() 列联表.
列联表.
甲班 | 乙班 | 合计 | |
优秀 | |||
不优秀 | |||
合计 |
(2)判断有多大把握认为“成绩优秀与教学方式有关”.
下面临界值表仅供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式: ![]()
【题目】A、B两种品牌各三种车型2017年7月的销量环比(与2017年6月比较)增长率如下表:
A品牌车型 | A1 | A2 | A3 | ||||
环比增长率 | -7.29% | 10.47% | 14.70% | ||||
B品牌车型 | B1 | B2 | B3 | ||||
环比增长率 | -8.49% | -28.06% | 13.25% | ||||
根据此表中的数据,有如下关于7月份销量的四个结论:①A1车型销量比B1车型销量多;
②A品牌三种车型总销量环比增长率可能大于14.70%;
③B品牌三款车型总销量环比增长率可能为正;
④A品牌三种车型总销量环比增长率可能小于B品牌三种车型总销量环比增长率.
其中正确结论的个数是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【题目】A、B两种品牌各三种车型2017年7月的销量环比(与2017年6月比较)增长率如下表:
A品牌车型 | A1 | A2 | A3 | ||||
环比增长率 | -7.29% | 10.47% | 14.70% | ||||
B品牌车型 | B1 | B2 | B3 | ||||
环比增长率 | -8.49% | -28.06% | 13.25% | ||||
根据此表中的数据,有如下关于7月份销量的四个结论:①A1车型销量比B1车型销量多;
②A品牌三种车型总销量环比增长率可能大于14.70%;
③B品牌三款车型总销量环比增长率可能为正;
④A品牌三种车型总销量环比增长率可能小于B品牌三种车型总销量环比增长率.
其中正确结论的个数是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()