题目内容
11.已知函数f(x)=lnx+ax的图象在x=1处的切线与直线2x-y-1=0垂直,则a=$-\frac{3}{2}$.分析 求导数,利用函数f(x)=lnx+ax的图象在x=1处的切线与直线2x-y-1=0垂直,列出方程,即可求出实数a的值.
解答 解:∵f(x)=lnx+ax,
∴f′(x)=$\frac{1}{x}$+a,
∵函数f(x)=lnx+ax的图象在x=1处的切线与直线2x-y-1=0垂直,
∴f′(1)=1+a=-$\frac{1}{2}$,
∴a=$-\frac{3}{2}$.
故答案为:$-\frac{3}{2}$.
点评 本题考查了导数的几何意义、切线的斜率、相互垂直的直线之间的斜率关系、恒成立问题的等价转化等基础知识与基本技能方法,属于中档题.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
16.曲线y=ax3-2bx+1在点(1,f(1))处的切线方程为y=-x+2,则a+2b=( )
| A. | -1 | B. | 1 | C. | 2 | D. | 3 |
1.已知集合M={x|(1-x)x>0},N={y|y=x2+2x+3},则(∁RM)∩N=( )
| A. | {x|0<x<1} | B. | {x|x>1} | C. | {x|x≥2} | D. | {x|1<x<2} |
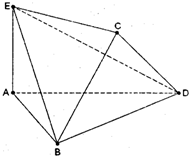 将边长为2的正方形ABCD沿对角线BD折叠,使得平面ABD⊥平面CBD,AE⊥平面ABD,且AE=$\frac{PC}{PA}=\frac{CA}{AB}$.
将边长为2的正方形ABCD沿对角线BD折叠,使得平面ABD⊥平面CBD,AE⊥平面ABD,且AE=$\frac{PC}{PA}=\frac{CA}{AB}$.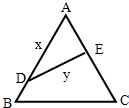 如图,某公园有一块边长为2的等边△ABC的边角地,现修成草坪,图中DE把草坪分成面积相等的两部分,D在AB上,E在AC上.
如图,某公园有一块边长为2的等边△ABC的边角地,现修成草坪,图中DE把草坪分成面积相等的两部分,D在AB上,E在AC上.