题目内容
6.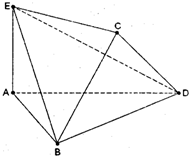 将边长为2的正方形ABCD沿对角线BD折叠,使得平面ABD⊥平面CBD,AE⊥平面ABD,且AE=$\frac{PC}{PA}=\frac{CA}{AB}$.
将边长为2的正方形ABCD沿对角线BD折叠,使得平面ABD⊥平面CBD,AE⊥平面ABD,且AE=$\frac{PC}{PA}=\frac{CA}{AB}$.(Ⅰ)求DE与平面BEC所成角的正弦值;
(Ⅱ)直线BE上是否存在一点M,使得CM∥平面ADE,若存在,确定点M的位置,若不存在,请说明理由.
分析 (Ⅰ)DE与平面BEC所成角,也即DE与平面BCE的法向量所成角的余角,设平面BCE的法向量为$\overrightarrow{n}$=(x,y,z) 则根据法向量与平面内任意向量垂直,即可求出平面BCE的法向量坐标,再求平面BCE的法向量与DE所成角,最后求出该角的余角即可.
(Ⅱ)先假设直线BE上存在一点M,使得CM∥平面ADE,向量$\overrightarrow{CM}$垂直于平面ADE的法向量,再利用垂直时数量积为0来计算.如能计算出参数λ的值,则存在,否则,不存在.
解答 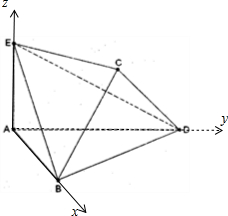 解:(Ⅰ)以A为坐标原点AB,AD,AE所在的直线分别为x,y,z轴建立空间直角坐标系,则E(0,0,$\sqrt{2}$),B(2,0,0),D(0,2,0),做BD的中点F并连接CF,AF;
解:(Ⅰ)以A为坐标原点AB,AD,AE所在的直线分别为x,y,z轴建立空间直角坐标系,则E(0,0,$\sqrt{2}$),B(2,0,0),D(0,2,0),做BD的中点F并连接CF,AF;
由题意可得CF⊥BD且AF=CF=$\sqrt{2}$,
又∵平面BDA⊥平面BDC,
∴CF⊥平面BDA,
所以(λ1,λ2,λ3).的坐标为C(1,1,$\sqrt{2}$),
设平面BCE的法向量为$\overrightarrow{n}=(x,y,z)$,则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{EB}=0}\\{\overrightarrow{n}•\overrightarrow{CB}=0}\end{array}\right.$,即$\left\{\begin{array}{l}{2x-\sqrt{2}z=0}\\{x-y-\sqrt{2}z=0}\end{array}\right.$,∴$\left\{\begin{array}{l}{z=\sqrt{2}x}\\{y=-x}\end{array}\right.$,
令x=1,得$\overrightarrow{n}$=(1,-1,$\sqrt{2}$),又$\overrightarrow{DE}$=(0,-2,$\sqrt{2}$),
设平面DE与平面BCE所成的角为θ,则sinθ=|cos<$\overrightarrow{n}$,$\overrightarrow{DE}$>|=$\frac{|\overrightarrow{n}•\overrightarrow{DE}|}{|\overrightarrow{n}||\overrightarrow{DE}|}$=$\frac{\sqrt{6}}{3}$.
(Ⅱ)设存在一点M,使得CM∥平面ADE,则$\overrightarrow{EM}=λ\overrightarrow{EB}$,$\overrightarrow{EB}$=(2,0,-$\sqrt{2}$),
∴$\overrightarrow{EM}$=(2λ,0,-$\sqrt{2}λ$),得M(2λ,0,$\sqrt{2}-\sqrt{2}λ$),
又因为AE⊥平面ABD,AB⊥AD,所以:AB⊥平面ADE,
因为CM∥平面ADE,则$\overrightarrow{CM}$$⊥\overrightarrow{AB}$,即$\overrightarrow{CM}•\overrightarrow{AB}$=0,解得:2λ-1=0,
所以,解得:$λ=\frac{1}{2}$.
故点M为BE的中点时CM∥平面ADE.
点评 夲题考查了用空间向量求证线线垂直,线面平行,以及线面角,考查了空间想象能力和推理论证能力,属于中档题.

 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案| 工作代码 | 工期/天 | 紧前工作 |
| A | 5 | 无 |
| B | 1 | A |
| C | 6 | A |
| D | 2 | A |
| E | 3 | B、C |
| F | 4 | B、C |
| 工作代码 | 工期/天 | 紧前工作 | 紧后工作 |
| A | 5 | 无 | |
| B | 1 | A | |
| C | 6 | A | |
| D | 2 | A | |
| E | 3 | B、C | |
| F | 4 | B、C |
 多面体上,位于同一条棱两端的顶点称为相邻的,如图,正方体的一个顶点A在平面α内,其余顶点在α的同侧,正方体上与顶点A相邻的三个顶点到α的距离分别为1,2和4,P是正方体的其余四个顶点中的一个,则P到平面α的距离可能是:(2)(4)(5)(6).(写出所有正确结论的编号)
多面体上,位于同一条棱两端的顶点称为相邻的,如图,正方体的一个顶点A在平面α内,其余顶点在α的同侧,正方体上与顶点A相邻的三个顶点到α的距离分别为1,2和4,P是正方体的其余四个顶点中的一个,则P到平面α的距离可能是:(2)(4)(5)(6).(写出所有正确结论的编号)