题目内容
9.椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的四个顶点按逆时针排列顺序依次为A,B,C,D,若四边形ABCD的内切圆恰好过焦点,则椭圆的离心率e2为( )| A. | $\frac{{3-\sqrt{5}}}{2}$ | B. | $\frac{{3+\sqrt{5}}}{8}$ | C. | $\frac{{\sqrt{5}-1}}{2}$ | D. | $\frac{{1+\sqrt{5}}}{8}$ |
分析 根据题意,由四边形ABCD的性质,分析可得其内切圆的半径的大小,又有其内切圆内切圆恰好过椭圆的焦点,即c=r;代入数据,计算可得答案.
解答 解:根据题意,易得四边形ABCD为平行四边形,则其内切圆的圆心为坐标原点;
进而分析可得,四边形ABCD的内切圆半径为Rt△AOB中,斜边AB上的高,
根据题意,易得,AO=a,OB=b,则r=$\frac{ab}{\sqrt{{a}^{2}+{b}^{2}}}$.
根据题意,其内切圆恰好过椭圆的焦点,
即c=r=$\frac{ab}{\sqrt{{a}^{2}+{b}^{2}}}$,即a2b2=c2(a2+b2)
又由a2=b2+c2;
则有a2(a2-c2)=c2(2a2-c2),
a4-3a2c2+c4=0,
解得:$\frac{{c}^{2}}{{a}^{2}}$=$\frac{3-\sqrt{5}}{2}$或$\frac{{c}^{2}}{{a}^{2}}$=$\frac{3+\sqrt{5}}{2}$
因为椭圆的离心率的取值范围为0<e<1.
所以e2=$\frac{3-\sqrt{5}}{2}$
故选:A.
点评 本题考查椭圆的性质,涉及平行四边形的有关性质,注意将椭圆的性质与平行四边形的性质结合起来运用,可以简化运算.

练习册系列答案
相关题目
18.已知点P在椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上,F1F2分别是其左、右焦点,若|PF1|=2|PF2|,则该椭圆的离心率的取值范围是( )
| A. | (0,$\frac{1}{3}$] | B. | ($\frac{1}{3}$,1) | C. | (0,$\frac{1}{3}$) | D. | [$\frac{1}{3}$,1) |
19.已知直线l:x-y+m=0与椭圆C:$\frac{{x}^{2}}{2}$+y2=1交于不同的两点A,B,且线段AB的中点不在圆x2+y2=$\frac{5}{9}$内,则m的取值范围为( )
| A. | m≥1或m≤-1 | B. | -$\sqrt{3}$≤m≤-1或1≤≤m≤$\sqrt{3}$ | C. | -1≤m≤1 | D. | -$\sqrt{3}$<m≤-1或1≤m<$\sqrt{3}$ |
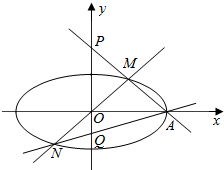 在平面直角坐标系xOy中,已知椭圆C的右顶点为A,两焦点坐标分别为(-$\sqrt{3}$,0)和($\sqrt{3}$,0),且经过点($\sqrt{3}$,$\frac{1}{2}$).过点O的直线交椭圆C于M、N两点,直线AM、AN分别交y轴于P、Q两点.
在平面直角坐标系xOy中,已知椭圆C的右顶点为A,两焦点坐标分别为(-$\sqrt{3}$,0)和($\sqrt{3}$,0),且经过点($\sqrt{3}$,$\frac{1}{2}$).过点O的直线交椭圆C于M、N两点,直线AM、AN分别交y轴于P、Q两点.