题目内容
已知函数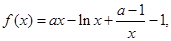 试讨论
试讨论 的单调性.
的单调性.
当 时
时 的减区间为
的减区间为 ,增区间为
,增区间为 ;当
;当 时,
时, 减函数为
减函数为 ,增区间为
,增区间为 和
和 ;当
;当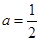 时;
时; 增区间为
增区间为 ,无减区间;当
,无减区间;当 时,
时, 的减区间为
的减区间为 ,增区间为
,增区间为 和
和 ;当
;当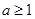 时,
时, 的减区间为
的减区间为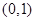 ,增区间为
,增区间为 .
.
解析试题分析:若要讨论 的单调性,先求出函数的定义域为
的单调性,先求出函数的定义域为 ,接着求导
,接着求导 ,这是一个含参的二次函数形式,讨论函数的单调性,则分
,这是一个含参的二次函数形式,讨论函数的单调性,则分 三种情况,当
三种情况,当 时分
时分 三种情况讨论.最后汇总一下分类讨论的情况.
三种情况讨论.最后汇总一下分类讨论的情况.
试题解析:函数的定义域为
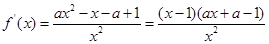
当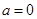 时
时 ,
, 的减区间为
的减区间为 ,增区间为
,增区间为 ;
;
当 时,令
时,令 得
得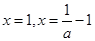 ;
;
当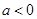 时,
时, 的减区间为
的减区间为 ,增区间为
,增区间为 ;
;
当 时,
时, 减函数为
减函数为 ,增区间为
,增区间为 和
和
当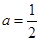 时,
时, 增区间为
增区间为 ,无减区间;
,无减区间;
当 时,
时, 的减区间为
的减区间为 ,增区间为
,增区间为 和
和 ;
;
当 时,
时, ,
, 的减区间为
的减区间为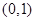 ,增区间为
,增区间为 .
.
综上,当 时
时 的减区间为
的减区间为 ,增区间为
,增区间为 ;
;
当 时,
时, 减函数为
减函数为 ,增区间为
,增区间为 和
和 ;
;
当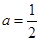 时;
时; 增区间为
增区间为 ,无减区间;
,无减区间;
当 时,
时, 的减区间为
的减区间为 ,增区间为
,增区间为 和
和 ;
;
当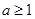 时,
时, 的减区间为
的减区间为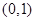 ,增区间为
,增区间为 .
.
考点:1.含参函数的求导判断单调性;2.分类讨论思想的应用.

练习册系列答案
相关题目
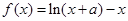 的最大值为0,其中
的最大值为0,其中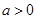 。
。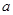 的值;
的值; 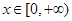 ,有
,有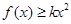 成立,求实数
成立,求实数 的最大值;
的最大值;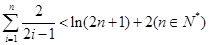
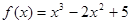 的定义域为区间
的定义域为区间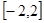 .
. 的极大值与极小值;
的极大值与极小值;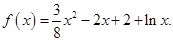
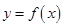 的单调区间;
的单调区间;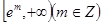 上有零点,求
上有零点,求 的最大值.
的最大值.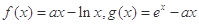 ,其中a为正实数.
,其中a为正实数.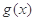 的极值点,讨论函数
的极值点,讨论函数 的单调性;
的单调性; 上无最小值,且
上无最小值,且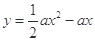 在
在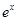 +3
+3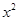 -ax.
-ax.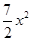 +ax+1在x≥
+ax+1在x≥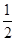 时恒成立,试求实数a的取值范围.
时恒成立,试求实数a的取值范围. .
. 在
在 上恒成立,求m取值范围;
上恒成立,求m取值范围;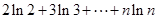
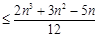 (
(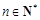 ).
).  )
)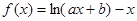 ,其中
,其中 ,
, ,
,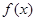 为
为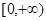 上的减函数,求
上的减函数,求 应满足的关系;
应满足的关系;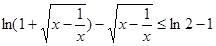 。
。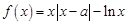 ,
,
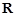 .
.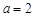 ,求函数
,求函数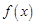 在区间
在区间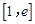 上的最值;
上的最值;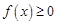 恒成立,求
恒成立,求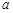 的取值范围. 注:
的取值范围. 注: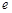 是自然对数的底数.
是自然对数的底数.