题目内容
已知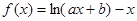 ,其中
,其中 ,
, ,
,
(Ⅰ)若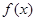 为
为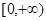 上的减函数,求
上的减函数,求 应满足的关系;
应满足的关系;
(Ⅱ)解不等式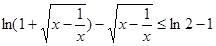 。
。
(Ⅰ)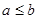 ;(Ⅱ)所求不等式的解集为
;(Ⅱ)所求不等式的解集为 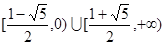 .
.
解析试题分析:(Ⅰ)若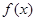 为
为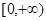 上的减函数,由于
上的减函数,由于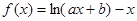 其中
其中 ,
, ,由于
,由于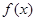 含有对数函数,可考虑它的导函数在
含有对数函数,可考虑它的导函数在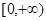 小于等于零恒成立,因此对
小于等于零恒成立,因此对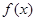 求导,得
求导,得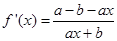 ,令
,令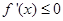 对
对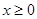 恒成立,只要
恒成立,只要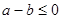 即可,从而得
即可,从而得 的关系;(Ⅱ)解不等式
的关系;(Ⅱ)解不等式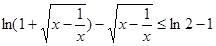 ,而
,而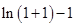 ,这样不等式两边的形式是
,这样不等式两边的形式是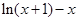 ,故对
,故对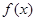 中取
中取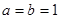 ,得
,得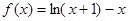 ,由(Ⅰ)知
,由(Ⅰ)知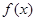 在
在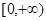 上是减函数,不等式
上是减函数,不等式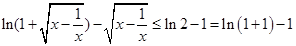 ,也就是
,也就是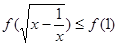 ,利用单调性得
,利用单调性得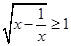 ,这样就可以解不等式.
,这样就可以解不等式.
试题解析:(Ⅰ)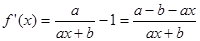 2分
2分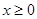
 ,
,
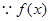 为
为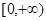 上的减函数
上的减函数 对
对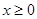 恒成立,
恒成立,
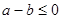 即
即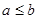 4分
4分
(Ⅱ)在(Ⅰ)中取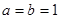 ,即
,即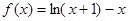 ,由(Ⅰ)知
,由(Ⅰ)知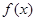 在
在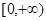 上是减函数,
上是减函数,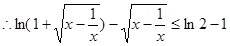 即
即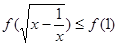 8分
8分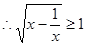 ,解得
,解得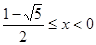 , 或
, 或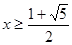
故所求不等式的解集为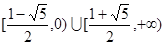 12分
12分
考点:函数与导数,函数单调性,利用单调性解不等式.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
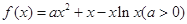 .
.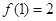 ,且在定义域内
,且在定义域内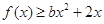 恒成立,求实数b的取值范围;
恒成立,求实数b的取值范围;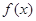 在定义域上是单调函数,求实数
在定义域上是单调函数,求实数 的取值范围;
的取值范围;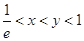 时,试比较
时,试比较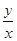 与
与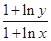 的大小.
的大小.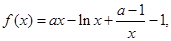 试讨论
试讨论 的单调性.
的单调性.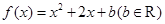 .
. 的值域为
的值域为 .求关于
.求关于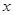 的不等式
的不等式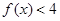 的解集;
的解集;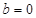 时,
时,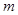 为常数,且
为常数,且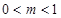 ,
,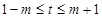 ,求
,求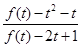 的最小值.
的最小值.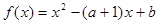 ,
, 的解集是
的解集是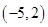 ,求
,求 的值;
的值;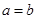 ,解关于
,解关于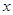 的不等式
的不等式 .
.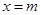 和
和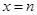 是函数
是函数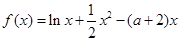 的两个极值点,其中
的两个极值点,其中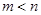 ,
,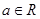 .
.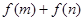 的取值范围;
的取值范围; 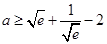 ,求
,求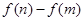 的最大值(e是自然对数的底数).
的最大值(e是自然对数的底数). ,其中
,其中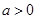 .
. ,求曲线
,求曲线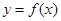 在点
在点 处的切线方程;
处的切线方程; 有三个零点,求
有三个零点,求 的取值范围.
的取值范围. ,
, .
. ,函数
,函数 与
与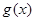 的图象在
的图象在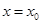 处的切线斜率总相等,求
处的切线斜率总相等,求 的值;
的值; ,对任意
,对任意 ,不等式
,不等式 恒成立,求实数
恒成立,求实数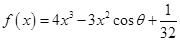 ,其中
,其中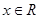 ,
,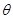 为参数,且
为参数,且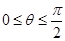 .
.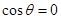 时,判断函数
时,判断函数 是否有极值;
是否有极值;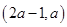 内都是增函数,求实数
内都是增函数,求实数 的取值范围.
的取值范围.