题目内容
已知函数f(x)=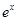 +3
+3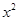 -ax.
-ax.
(1)若f(x)在x=0处取得极值,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)若关于x的不等式f(x)≥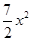 +ax+1在x≥
+ax+1在x≥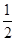 时恒成立,试求实数a的取值范围.
时恒成立,试求实数a的取值范围.
(Ⅰ)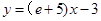 ;(II)
;(II)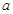 的取值范围是
的取值范围是 .
.
解析试题分析:(Ⅰ)由题可知,函数的导函数在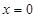 处函数值为零,故可求得
处函数值为零,故可求得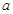 的值,故而得到函数的解析式,然后利用导数求出(1,f(1))的斜率,利用点斜式写出切线方程;(II)由(Ⅰ)已知了函数解析式,将给出的不等式分离参数,构造函数求出参数的范围.
的值,故而得到函数的解析式,然后利用导数求出(1,f(1))的斜率,利用点斜式写出切线方程;(II)由(Ⅰ)已知了函数解析式,将给出的不等式分离参数,构造函数求出参数的范围.
试题解析:(Ⅰ) , ∵
, ∵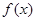 在
在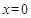 处取得极值,
处取得极值, , 2分
, 2分
则
 4分
4分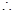 曲线
曲线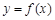 在点
在点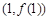 处的切线方程为:
处的切线方程为: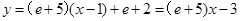 . 5分
. 5分
(II)由 ,得
,得 ,
,
即 ,∵
,∵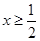 ,∴
,∴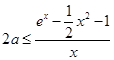 , 7分
, 7分
令 , 则
, 则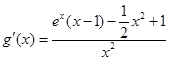 . 8分
. 8分
令 ,则
,则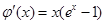 .
.
∵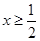 ,∴
,∴ ,∴
,∴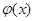 在
在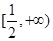 上单调递增, 10分
上单调递增, 10分
∴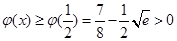 ,因此
,因此 ,故
,故 在
在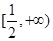 上单调递增,
上单调递增,
则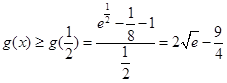 ,∴
,∴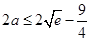 ,
,
即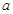 的取值范围是
的取值范围是 . 12分
. 12分
考点:导数的几何意义、直线方程、分离参数法、利用导数求函数最值.

练习册系列答案
相关题目
 .
.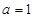 时,求曲线
时,求曲线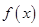 在
在 处的切线方程;
处的切线方程;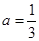 时,求函数
时,求函数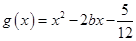 ,若对于
,若对于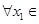 [1,2],
[1,2], [0,1],使
[0,1],使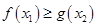 成立,求实数
成立,求实数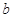 的取值范围.
的取值范围.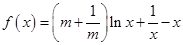 ,(其中常数
,(其中常数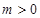 ).
).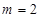 时,求
时,求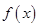 的极大值;
的极大值;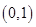 上的单调性;
上的单调性;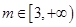 时,曲线
时,曲线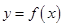 上总存在相异两点
上总存在相异两点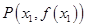 、
、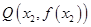 ,使得曲线
,使得曲线 、
、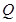 处的切线互相平行,求
处的切线互相平行,求 的取值范围.
的取值范围. 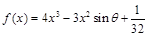 ,其中
,其中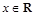 ,
,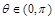 .
.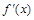 的最小值为
的最小值为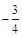 ,试判断函数
,试判断函数 的零点个数,并说明理由;
的零点个数,并说明理由;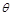 的取值范围.
的取值范围.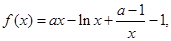 试讨论
试讨论 的单调性.
的单调性.
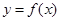 在点
在点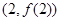 处的切线方程;
处的切线方程; 的极值;
的极值; 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.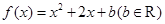 .
. 的值域为
的值域为 .求关于
.求关于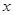 的不等式
的不等式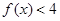 的解集;
的解集;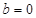 时,
时,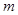 为常数,且
为常数,且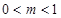 ,
,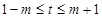 ,求
,求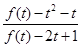 的最小值.
的最小值.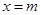 和
和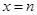 是函数
是函数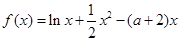 的两个极值点,其中
的两个极值点,其中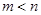 ,
,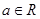 .
.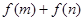 的取值范围;
的取值范围; 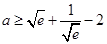 ,求
,求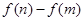 的最大值(e是自然对数的底数).
的最大值(e是自然对数的底数).
 时,求f(x)的单调区间;
时,求f(x)的单调区间;