题目内容
[2014·济宁模拟]若函数f(x)＝|2x＋a|的单调递增区间是[3，＋∞)，则a＝________.
－6
由图象的对称性，知函数f(x)＝|2x＋a|关于直线x＝－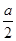
对称，因为函数f(x)＝|2x＋a|的单调递增区间是[3，＋∞)，所以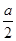－＝3，即a＝－6.
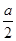对称，因为函数f(x)＝|2x＋a|的单调递增区间是[3，＋∞)，所以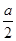－＝3，即a＝－6.
练习册系列答案
阅读快车系列答案
相关题目
阅读快车系列答案题目内容
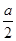对称，因为函数f(x)＝|2x＋a|的单调递增区间是[3，＋∞)，所以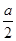－＝3，即a＝－6.阅读快车系列答案
是函数
图像上的任意一点，点
，则
、
两点之间距离的最小值是______________.
，则f(x)的单调递减区间是( )
与y＝log3(x－2)在(3，＋∞)上具有相同的单调性，则实数k的取值范围是________．
是定义在R上的偶函数，且当
时，
。若对任意的x
，不等式
恒成立，则实数a的最大值是（ ）。
<f(1)
的最大值为（ ）
