题目内容
函数f(x)＝(x－3)ex的单调递增区间是( )
| A．(－∞，2) | B．(0,3) | C．(1,4) | D．(2，＋∞) |
D
函数f(x)＝(x－3)ex的导数为f′(x)＝[(x－3)ex]′＝1·ex＋(x－3)·ex＝(x－2)ex.由函数导数与函数单调性的关系，得当f′(x)>0时，函数f(x)单调递增，此时由不等式f′(x)＝(x－2)·ex>0，解得x>2.
练习册系列答案
教材全解字词句篇系列答案
相关题目
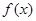是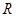
上的奇函数，且当
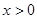时，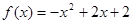
.
.
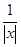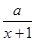在区间[1,2]上都是减函数，则a的取值范围是________．
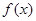在[0，+∞]上是增函数，
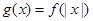，若
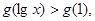则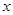
的取值范围是（ ）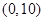
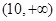
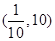
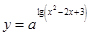有最大值，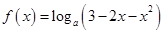
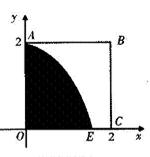
的单调区间．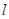
（宽度不计），切点为M，并把该地块分为两部分．现以点O为坐标原点，以线段OC所在直线为x轴，建立平面直角坐标系，若池边AE满足函数
）的图象，且点M到边OA距离为
．
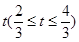时，求直路