题目内容
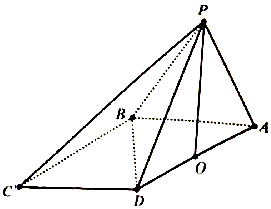
【题目】如图,正方形ABCD与正方形BCEF所成角的二面角的平面角的大小是 ![]() ,PQ是正方形BDEF所在平面内的一条动直线,则直线BD与PQ所成角的取值范围是( )
,PQ是正方形BDEF所在平面内的一条动直线,则直线BD与PQ所成角的取值范围是( ) 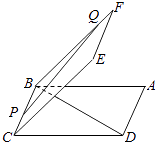
A.[ ![]() ,
, ![]() ]
]
B.[ ![]() ,
, ![]() ]
]
C.[ ![]() ,
, ![]() ]
]
D.[ ![]() ,
, ![]() ]
]
【答案】B
【解析】解:以B为原点,BC为x轴,BA为y轴,过B作平面ABCD的垂线为z轴,建立空间直角坐标系,
设BC=1,则B(0,0,0),D(1,1,0),C(1,0,0),
E(1, ![]() ,
, ![]() ),F(0,
),F(0, ![]() ,
, ![]() ),
),
当D点在正方形BCEF的投影刚好落在CE上,记为G点,其坐标为G(1, ![]() ,
, ![]() ),
),
此时BG与BD所成角刚好30度,
即直线BD与PQ所成角的最小值为 ![]() ,
,
取P( ![]() ,0,0),Q(0,
,0,0),Q(0, ![]() ,
, ![]() )时,直线BD于PQ所成角取最大值,
)时,直线BD于PQ所成角取最大值,
∵ ![]() =(1,1,0),
=(1,1,0), ![]() =(﹣
=(﹣ ![]() ,
, ![]() ,
, ![]() ),
),
∴cos< ![]() >=
>= 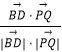 =0,
=0,
∴直线BD于PQ所成角最大值为 ![]() .
.
∴直线BD与PQ所成角的取值范围是[ ![]() ,
, ![]() ].
].
故选:B.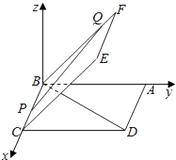
【考点精析】本题主要考查了异面直线及其所成的角的相关知识点,需要掌握异面直线所成角的求法:1、平移法:在异面直线中的一条直线中选择一特殊点,作另一条的平行线;2、补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系才能正确解答此题.

练习册系列答案
相关题目