题目内容
【题目】如图,在四棱锥P﹣ABCD中,PC⊥平面ABCD,AB∥DC,DC⊥AC.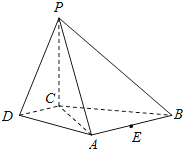
(1)求证:DC⊥平面PAC;
(2)求证:平面PAB⊥平面PAC;
(3)设点E为AB的中点,在棱PB上是否存在点F,使得PA∥平面CEF?说明理由.
【答案】
(1)
证明:∵PC⊥平面ABCD,DC平面ABCD,
∴PC⊥DC,
∵DC⊥AC,PC∩AC=C,
∴DC⊥平面PAC;
(2)
证明:∵AB∥DC,DC⊥AC,
∴AB⊥AC,
∵PC⊥平面ABCD,AB平面ABCD,
∴PC⊥AB,
∵PC∩AC=C,
∴AB⊥平面PAC,
∵AB平面PAB,
∴平面PAB⊥平面PAC;
(3)
解:在棱PB上存在中点F,使得PA∥平面CEF.
∵点E为AB的中点,
∴EF∥PA,
∵PA平面CEF,EF平面CEF,
∴PA∥平面CEF
【解析】(1)利用线面垂直的判定定理证明DC⊥平面PAC;
(2)利用线面垂直的判定定理证明AB⊥平面PAC,即可证明平面PAB⊥平面PAC;
(3)在棱PB上存在中点F,使得PA∥平面CEF.利用线面平行的判定定理证明.
本题考查线面平行与垂直的证明,考查平面与平面垂直的证明,考查学生分析解决问题的能力,属于中档题.
【考点精析】本题主要考查了空间中直线与平面之间的位置关系和平面与平面之间的位置关系的相关知识点,需要掌握直线在平面内—有无数个公共点;直线与平面相交—有且只有一个公共点;直线在平面平行—没有公共点;两个平面平行没有交点;两个平面相交有一条公共直线才能正确解答此题.

练习册系列答案
相关题目