题目内容
已知函数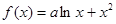 (
(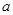 为实常数) .
为实常数) .
(1)当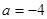 时,求函数
时,求函数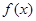 在
在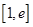 上的最大值及相应的
上的最大值及相应的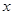 值;
值;
(2)当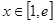 时,讨论方程
时,讨论方程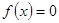 根的个数.
根的个数.
(3)若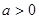 ,且对任意的
,且对任意的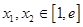 ,都有
,都有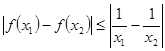 ,求实数a的取值范围.
,求实数a的取值范围.
(1)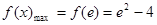 .
.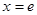 ;(2)
;(2)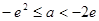 时,方程
时,方程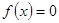 有2个相异的根.
有2个相异的根. 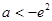 或
或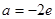 时,方程
时,方程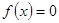 有1个根.
有1个根. 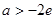 时,方程
时,方程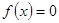 有0个根.(3)
有0个根.(3)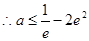 .
.
解析试题分析:(1)通过求导数可得函数的单调性,在对比区间的两端点的函数值即可求得函数的最大值.(2)由于参数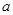 的变化.可以采取分离变量的方法,转化为两个函数的交点个数问题.其中一个是垂直于y轴的直线,另一个是通过求出函数的走向.根据图像即可得到结论.(3)将要说明的结论通过变形得到一个等价问题从而证明新的函数的单调性,使得问题巧妙地转化.本题只是容量大.通过研究函数的单调性,含参函数的讨论.与不等式的相结合转化为函数的单调性的证明.
的变化.可以采取分离变量的方法,转化为两个函数的交点个数问题.其中一个是垂直于y轴的直线,另一个是通过求出函数的走向.根据图像即可得到结论.(3)将要说明的结论通过变形得到一个等价问题从而证明新的函数的单调性,使得问题巧妙地转化.本题只是容量大.通过研究函数的单调性,含参函数的讨论.与不等式的相结合转化为函数的单调性的证明.
试题解析:(1)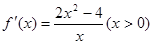 ,当
,当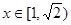 时,
时,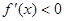 .当
.当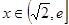 时,
时,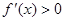 ,又
,又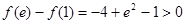 ,
,
故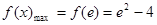 ,当
,当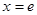 时,取等号 4分
时,取等号 4分
(2)易知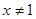 ,故
,故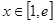 ,方程
,方程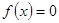 根的个数等价于
根的个数等价于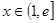 时,方程
时,方程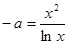 根的个数. 设
根的个数. 设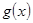 =
=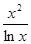 ,
, 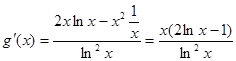
当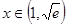 时,
时,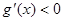 ,函数
,函数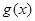 递减,当
递减,当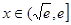 时,
时,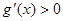 ,函数
,函数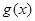 递增.又
递增.又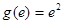 ,
,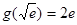 ,作出
,作出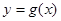 与直线
与直线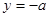 的图像,由图像知:
的图像,由图像知:
当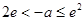 时,即
时,即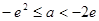 时,方程
时,方程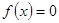 有2个相异的根;
有2个相异的根;
当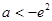 或
或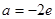 时,方程
时,方程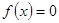 有1个根;
有1个根;
当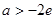 时,方程
时,方程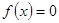 有0个根; 10分
有0个根; 10分
(3)当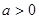 时,
时,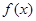 在
在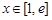 时是增函数,又函数
时是增函数,又函数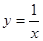 是减函数,不妨设
是减函数,不妨设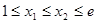 ,则
,则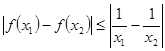 等价于
等价于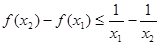
即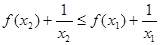 ,故原题等价于函数
,故原题等价于函数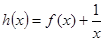 在
在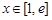 时是减函数,
时是减函数,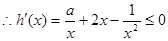 恒成立,即
恒成立,即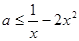 在
在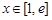 时恒成立.
时恒成立.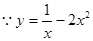 在
在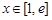 时是减函数
时是减函数 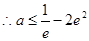 16分
16分
(其他解法酌情给分)
考点:1.函数的最值问题.2.函数的单调性.3.函数与不等式的关系以及转化为函数的单调性的证明.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
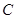 :
: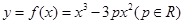 .
.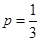 时,求曲线
时,求曲线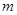 的两条直线与曲线
的两条直线与曲线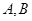 两点,求证:
两点,求证: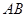 中点
中点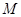 在曲线
在曲线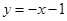 ,求
,求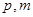 的值.
的值. 的前
的前 项和为
项和为 ,已知
,已知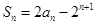 (n∈N*).
(n∈N*).
 ,数列
,数列 的前
的前 项和为
项和为 .利用(2)的结论证明:当n∈N*且n≥2时,
.利用(2)的结论证明:当n∈N*且n≥2时, .
.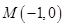 、
、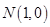 ,点
,点 为坐标平面内的动点,满足
为坐标平面内的动点,满足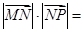
 .
.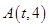 是动点
是动点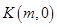 是
是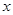 轴上的一动点,试讨论直线
轴上的一动点,试讨论直线 与圆
与圆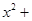
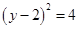 的位置关系.
的位置关系.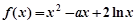 (其中
(其中 是实数).
是实数).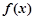 的单调区间;
的单调区间; ,且
,且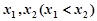 ,求
,求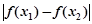 的取值范围.
的取值范围.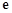 是自然对数的底数)
是自然对数的底数) ,
, .
. 时,函数
时,函数 取得极值,求
取得极值,求 的值;
的值; 时,求函数
时,求函数 时,关于
时,关于 的方程
的方程
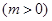 有唯一实数解,求实数
有唯一实数解,求实数 的值.
的值.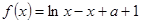
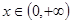 使得
使得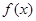 ≥0成立,求
≥0成立,求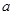 的范围
的范围  >1时,在(1)的条件下,
>1时,在(1)的条件下,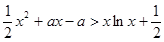 成立
成立
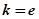 ,试确定函数
,试确定函数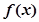 的单调区间;
的单调区间;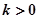 且对任意
且对任意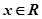 ,
,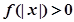 恒成立,试确定实数
恒成立,试确定实数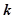 的取值范围;
的取值范围;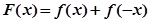 ,求证:
,求证: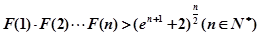
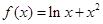 .
.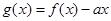 在定义域内为增函数,求实数
在定义域内为增函数,求实数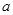 的取值范围;
的取值范围;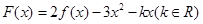 ,若函数
,若函数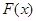 存在两个零点
存在两个零点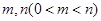 ,且实数
,且实数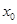 满足
满足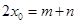 ,问:函数
,问:函数 处的切线能否平行于
处的切线能否平行于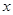 轴?若能,求出该切线方程;若不能,请说明理由.
轴?若能,求出该切线方程;若不能,请说明理由.