题目内容
已知曲线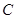 :
: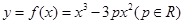 .
.
(Ⅰ)当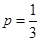 时,求曲线
时,求曲线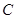 的斜率为1的切线方程;
的斜率为1的切线方程;
(Ⅱ)设斜率为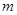 的两条直线与曲线
的两条直线与曲线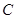 相切于
相切于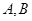 两点,求证:
两点,求证: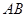 中点
中点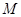 在曲线
在曲线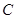 上;
上;
(Ⅲ)在(Ⅱ)的条件下,又已知直线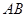 的方程为:
的方程为: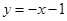 ,求
,求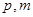 的值.
的值.
(Ⅰ)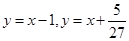 ;(Ⅱ)详见解析;(Ⅲ)
;(Ⅱ)详见解析;(Ⅲ)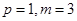 .
.
解析试题分析:(Ⅰ)当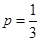 时,先求导,通过斜率为1得到切点.然后利用点斜式得到所求切线方程;(Ⅱ)先将
时,先求导,通过斜率为1得到切点.然后利用点斜式得到所求切线方程;(Ⅱ)先将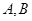 两点的坐标设出,其中纵坐标用相应点的横坐标表示.再由导数的几何意义,得到
两点的坐标设出,其中纵坐标用相应点的横坐标表示.再由导数的几何意义,得到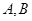 两点横坐标满足
两点横坐标满足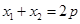 .从而得到
.从而得到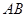 中点
中点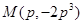 ,又
,又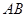 中点
中点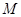 在曲线
在曲线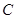 上
上 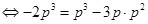 ,显然成立.得证;(Ⅲ)由
,显然成立.得证;(Ⅲ)由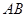 中点在直线
中点在直线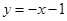 ,又在曲线
,又在曲线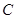 ,从而得
,从而得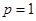 ,再反代如直线与曲线联立得方程,得到
,再反代如直线与曲线联立得方程,得到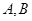 两点的坐标,代入导函数中得到斜率,从而得到
两点的坐标,代入导函数中得到斜率,从而得到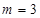 .
.
试题解析:(Ⅰ)当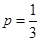 时,
时,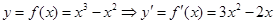 ,
,
设切点为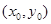 ,由
,由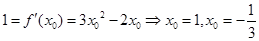 ,切点为
,切点为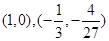
故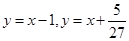 为所求. (4分)
为所求. (4分)
(Ⅱ)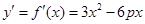 ,设
,设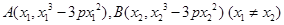 ,
,
由导数的几何意义有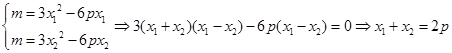

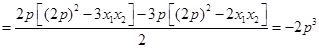
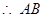 中点
中点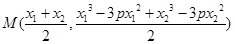 ,即
,即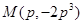 ,
,
又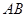 中点
中点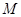 在曲线
在曲线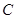 上
上 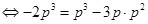 ,显然成立.得证. (8分)
,显然成立.得证. (8分)
(Ⅲ)由(Ⅱ)知,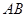 中点
中点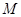 的横坐标为
的横坐标为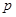 ,且
,且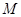 在
在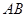 上,
上,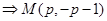 ,
,
又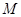 在曲线
在曲线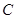 上,
上,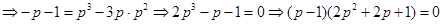 ,
,
所以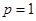 .
.
由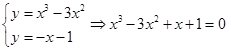 ,
,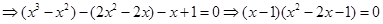
由于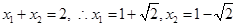 ,
,
故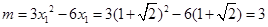 .
.
综上,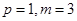 为所求. (13分)
为所求. (13分)
考点:1.导数的几何意义;2.直线的方程;3.直线与曲线的位置关系.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 .
.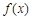 在(0,+∞)内的极值;
在(0,+∞)内的极值;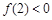 ,
,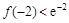 ,且
,且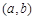 形成的平面区域的面积.
形成的平面区域的面积.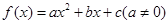 ,曲线
,曲线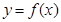 通过点(0,2a+3),且在
通过点(0,2a+3),且在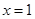 处的切线垂直于y轴.
处的切线垂直于y轴.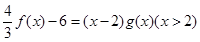 ,求g(x)的最大值及相应x值.
,求g(x)的最大值及相应x值. (
( 为自然对数的底数)。
为自然对数的底数)。 ,求函数
,求函数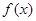 的单调区间;
的单调区间; ,使函数
,使函数 上是单调增函数?若存在,求出
上是单调增函数?若存在,求出
 ,又
,又 ,
,
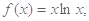
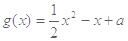 .
.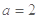 时,求
时,求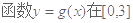 上的值域;
上的值域;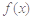 在
在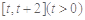 上的最小值;
上的最小值;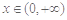 ,都有
,都有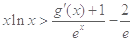 成立
成立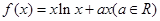 .
.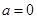 ,求
,求 的最小值;
的最小值;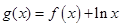 在区间
在区间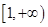 上为增函数,求实数
上为增函数,求实数 的取值范围;
的取值范围;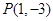 恰好能作函数
恰好能作函数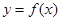 图象的两条切线,并且两切线的倾斜角互补,求实数
图象的两条切线,并且两切线的倾斜角互补,求实数
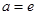 时,求
时,求 在
在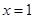 处的切线方程;
处的切线方程;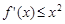 对任意的
对任意的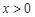 恒成立,求实数
恒成立,求实数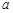 的取值范围;
的取值范围;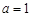 时,设函数
时,设函数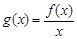 ,若
,若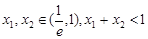 ,求证:
,求证: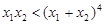 .
.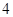 元,并且每件商品需向总店交
元,并且每件商品需向总店交 元的管理费,预计当每件商品的售价为
元的管理费,预计当每件商品的售价为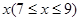 元时,一年的销售量为
元时,一年的销售量为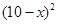 万件.
万件.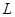 (万元)与每件商品的售价
(万元)与每件商品的售价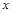 的函数关系式
的函数关系式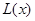 ;
;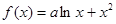 (
(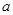 为实常数) .
为实常数) .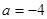 时,求函数
时,求函数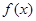 在
在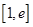 上的最大值及相应的
上的最大值及相应的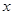 值;
值;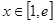 时,讨论方程
时,讨论方程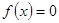 根的个数.
根的个数.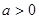 ,且对任意的
,且对任意的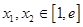 ,都有
,都有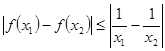 ,求实数a的取值范围.
,求实数a的取值范围.