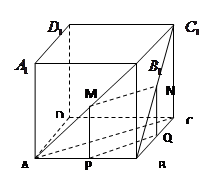
题目内容
正方体 中,点
中,点 分别在线段
分别在线段 上,且
上,且  .以下结论:①
.以下结论:① ;②
;② ;③MN//平面
;③MN//平面 ;④MN与
;④MN与 异面;⑤MN⊥平面
异面;⑤MN⊥平面 .其中有可能成立的结论的个数为( )
.其中有可能成立的结论的个数为( )

 中,点
中,点 分别在线段
分别在线段 上,且
上,且  .以下结论:①
.以下结论:① ;②
;② ;③MN//平面
;③MN//平面 ;④MN与
;④MN与 异面;⑤MN⊥平面
异面;⑤MN⊥平面 .其中有可能成立的结论的个数为( )
.其中有可能成立的结论的个数为( )| A.5 | B.4 | C.3 | D.2 |

A
 |
作
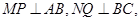 垂足是
垂足是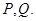
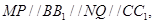
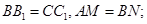

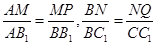 则
则
 是平行四边形;
是平行四边形;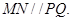
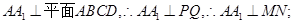
当
 分别是线段
分别是线段 的中点时,
的中点时,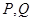 分别是
分别是 的中点;此时
的中点;此时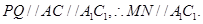
 则
则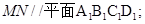
当
 在
在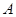 点时,
点时,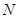 在点
在点 此时
此时 与
与 异面;
异面;当
 分别是线段
分别是线段 的中点时,
的中点时,
 故选A.
故选A.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
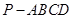 的底面是正方形,
的底面是正方形,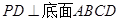 ,点E在棱PB上,O为AC与BD的交点。
,点E在棱PB上,O为AC与BD的交点。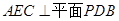 ;
; 2)当E为PB中点时,求证:
2)当E为PB中点时,求证: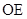 //平面PDA,
//平面PDA,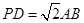 且E为PB的中点时,求
且E为PB的中点时,求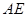 与平面
与平面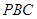 所成的角的大小。
所成的角的大小。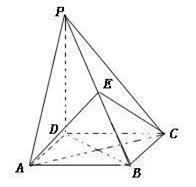

 的大小。
的大小。 倍,P为侧棱SD上的点。
倍,P为侧棱SD上的点。
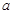 与平面
与平面 没有公共点,则
没有公共点,则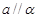 ;
; ,则
,则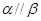
 是直角梯形,∠
是直角梯形,∠ =90°,
=90°, ∥
∥ ,
, =1,∠
=1,∠ =120°,
=120°, ⊥
⊥ ,直线
,直线 与直线
与直线 ⊥平面
⊥平面 ;
; 的体积;
的体积;
 中,
中, 分别为BC, CC1中点,
分别为BC, CC1中点, 与
与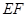 所成角的大小为
所成角的大小为







