题目内容
20.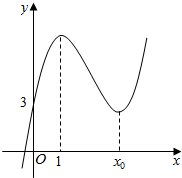 已知函数f(x)=ax3+bx2+(c-3a-2b)x+d(a>0)的图象如图所示,该函数的单调增区间为(-∞,1)和(x0,+∞),单调减区间为(1,x0).
已知函数f(x)=ax3+bx2+(c-3a-2b)x+d(a>0)的图象如图所示,该函数的单调增区间为(-∞,1)和(x0,+∞),单调减区间为(1,x0).(1)求c,d的值;
(2)若x0=5,方程f(x)=8a有三个不同的根,求实数a的取值范围.
分析 (1)求导函数,利用函数f(x)的图象过点(0,3),且f′(1)=0,建立方程,即可求c,d的值;
(2)先求出b=-9a,问题转化为ax2-6ax+5=0有2个不同的实根,根据根的判别式得到不等式解出即可.
解答 解:函数f(x)的导函数为f′(x)=3ax2+2bx+c-3a-2b,
(1)由图可知,函数f(x)的图象过点(0,3),且f′(1)=0,
∴$\left\{\begin{array}{l}{d=3}\\{3a+2b+c-3a-2b=0}\end{array}\right.$⇒$\left\{\begin{array}{l}{d=3}\\{c=0}\end{array}\right.$,
(2)由(1)得:f′(x)=3ax2+2bx-(3a+2b),
由题意得:1,5是方程f′(x)=0的2个根,
∴$\left\{\begin{array}{l}{-\frac{2b}{3a}=3}\\{-\frac{3a+2b}{3a}=5}\end{array}\right.$,解得:b=-9a,
∴f(x)=ax3-9ax2+15ax+3,
方程f(x)=8a有三个不同的根,
即方程ax3-9ax2+15ax+3-8a=0有三个不同的根,
令g(x)=ax3-9ax2+15ax+3-8a,
得:g′(x)=3(ax2-6ax+5),
问题转化为ax2-6ax+5=0有2个不同的实根,
∴△=36a2-20a>0,解得:a>$\frac{5}{9}$或a<0(舍).
点评 本题考查导数知识的综合运用,考查导数的几何意义,考查函数的解析式,属于中档题.

练习册系列答案
相关题目
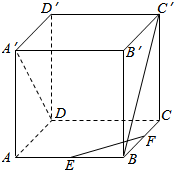 如图,正方体ABCD-A′B′C′D′的棱长为a,E,F分别是棱AB,BC的中点,求:
如图,正方体ABCD-A′B′C′D′的棱长为a,E,F分别是棱AB,BC的中点,求: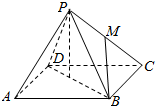 已知四边形ABCD为正方形,P为面ABCD外一点,且PA=PB=PC=PD=2,AB=$\sqrt{2}$,M是侧棱PC的中点,则异面直线PA与BM所成的角的大小为45°.
已知四边形ABCD为正方形,P为面ABCD外一点,且PA=PB=PC=PD=2,AB=$\sqrt{2}$,M是侧棱PC的中点,则异面直线PA与BM所成的角的大小为45°.