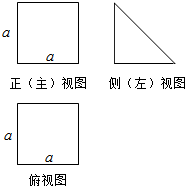
题目内容
13.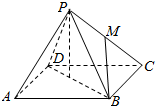 已知四边形ABCD为正方形,P为面ABCD外一点,且PA=PB=PC=PD=2,AB=$\sqrt{2}$,M是侧棱PC的中点,则异面直线PA与BM所成的角的大小为45°.
已知四边形ABCD为正方形,P为面ABCD外一点,且PA=PB=PC=PD=2,AB=$\sqrt{2}$,M是侧棱PC的中点,则异面直线PA与BM所成的角的大小为45°.
分析 连结AC,BD交于点O,连结OP,以O为原点,OA、OB、OC分别为x轴,y轴,z轴,建立空间直角坐标系,利用向量法能求出异面直线PA与BM所成的角的大小.
解答  解:连结AC,BD交于点O,连结OP,
解:连结AC,BD交于点O,连结OP,
∵四边形ABCD为正方形,P为面ABCD外一点,且PA=PB=PC=PD=2,AB=$\sqrt{2}$,M是侧棱PC的中点,
∴AC⊥BD,OP⊥AC,∴OP⊥AC,同理OP⊥BD,
以O为原点,OA、OB、OC分别为x轴,y轴,z轴,建立空间直角坐标系,
则P(0,0,$\sqrt{3}$),A(1,0,0),B(0,1,0),C(-1,0,0),
∴M(-$\frac{1}{2}$,0,$\frac{\sqrt{3}}{2}$),$\overrightarrow{AP}$=(-1,0,$\sqrt{3}$),$\overrightarrow{BM}$=(-$\frac{1}{2}$,-1,$\frac{\sqrt{3}}{2}$),
∴cos<$\overrightarrow{AP},\overrightarrow{BM}$>=$\frac{\frac{1}{2}+0+\frac{3}{2}}{\sqrt{1+0+3}•\sqrt{\frac{1}{4}+1+\frac{3}{4}}}$=$\frac{\sqrt{2}}{2}$,
∴异面直线PA与BM所成的角的大小为45°.
故答案为:45°.
点评 本题考查异面直线所成角的大小的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
2.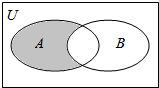 设全集U=R,A={x|2x-2<1},B={y|y=ln(1-x),x>1-e},则图中阴影部分表示的集合为( )
设全集U=R,A={x|2x-2<1},B={y|y=ln(1-x),x>1-e},则图中阴影部分表示的集合为( )
 设全集U=R,A={x|2x-2<1},B={y|y=ln(1-x),x>1-e},则图中阴影部分表示的集合为( )
设全集U=R,A={x|2x-2<1},B={y|y=ln(1-x),x>1-e},则图中阴影部分表示的集合为( )| A. | {x|x≥1} | B. | {x|1≤x<2} | C. | {x|0<x≤1} | D. | {x|x≤1} |
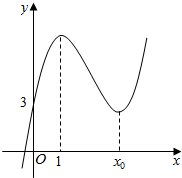 已知函数f(x)=ax3+bx2+(c-3a-2b)x+d(a>0)的图象如图所示,该函数的单调增区间为(-∞,1)和(x0,+∞),单调减区间为(1,x0).
已知函数f(x)=ax3+bx2+(c-3a-2b)x+d(a>0)的图象如图所示,该函数的单调增区间为(-∞,1)和(x0,+∞),单调减区间为(1,x0).