题目内容
8.函数f(x)=|2x-a|在(2,+∞)上单调递增,则实数a的取值范围是(-∞,4].分析 去绝对值号便可看出当$x>\frac{a}{2}$时,f(x)单调递增,从而根据f(x)在(2,+∞)上单调递增便有,$\frac{a}{2}≤2$,这样便可得出实数a的取值范围.
解答 解:f(x)=$\left\{\begin{array}{l}{2x-a}&{x>\frac{a}{2}}\\{-2x+a}&{x≤\frac{a}{2}}\end{array}\right.$;
∴f(x)在$(\frac{a}{2},+∞)$上单调递增;
又f(x)在(2,+∞)上单调递增;
∴$\frac{a}{2}≤2$;
∴a≤4;
∴实数a的取值范围是(-∞,4].
故答案为:(-∞,4].
点评 考查含绝对值函数的处理方法:去绝对值号,以及一次函数的单调性.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
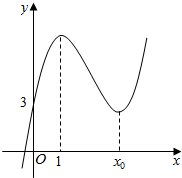 已知函数f(x)=ax3+bx2+(c-3a-2b)x+d(a>0)的图象如图所示,该函数的单调增区间为(-∞,1)和(x0,+∞),单调减区间为(1,x0).
已知函数f(x)=ax3+bx2+(c-3a-2b)x+d(a>0)的图象如图所示,该函数的单调增区间为(-∞,1)和(x0,+∞),单调减区间为(1,x0).