题目内容
5.利用夹逼准则计算下列极限.(1)$\underset{lim}{n→∞}$($\frac{1}{\sqrt{{n}^{2}+1}}+\frac{1}{\sqrt{{n}^{2}+2}}+…+\frac{1}{\sqrt{{n}^{2}+n}}$);
(2)$\underset{lim}{n→∞}$($\frac{1}{{n}^{2}}+\frac{1}{{(n+1)}^{2}}+…+\frac{1}{{2n}^{2}}$);
(3)$\underset{lim}{n→∞}$($\frac{1}{{n}^{2}+n+1}+\frac{2}{{n}^{2}+n+2}+…+\frac{n}{{n}^{2}+n+n}$).
分析 (1)由于$\frac{1}{\sqrt{1+\frac{1}{n}}}$=$\frac{n}{\sqrt{{n}^{2}+n}}$≤$\frac{1}{\sqrt{{n}^{2}+1}}+\frac{1}{\sqrt{{n}^{2}+2}}+…+\frac{1}{\sqrt{{n}^{2}+n}}$≤$\frac{n}{\sqrt{{n}^{2}+1}}$=$\frac{1}{\sqrt{1+\frac{1}{{n}^{2}}}}$;利用数列极限运算法则即可得出.
(2)由于$\frac{1}{2n}$=$\frac{n}{2{n}^{2}}$≤$\frac{1}{{n}^{2}}+\frac{1}{{(n+1)}^{2}}+…+\frac{1}{{2n}^{2}}$≤$\frac{n}{{n}^{2}}$=$\frac{1}{n}$;利用数列极限运算法则即可得出.
(3)由于$\frac{1+\frac{1}{n}}{2(1+\frac{2}{n})}$=$\frac{1+2+…+n}{{n}^{2}+n+n}$≤$\frac{1}{{n}^{2}+n+1}+\frac{2}{{n}^{2}+n+2}+…+\frac{n}{{n}^{2}+n+n}$≤$\frac{1+2+…+n}{{n}^{2}+n+1}$=$\frac{n(n+1)}{2({n}^{2}+n+1)}$=$\frac{1+\frac{1}{n}}{2(1+\frac{1}{n}+\frac{1}{{n}^{2}})}$,利用数列极限运算法则即可得出.
解答 解:(1)∵$\frac{1}{\sqrt{1+\frac{1}{n}}}$=$\frac{n}{\sqrt{{n}^{2}+n}}$≤$\frac{1}{\sqrt{{n}^{2}+1}}+\frac{1}{\sqrt{{n}^{2}+2}}+…+\frac{1}{\sqrt{{n}^{2}+n}}$≤$\frac{n}{\sqrt{{n}^{2}+1}}$=$\frac{1}{\sqrt{1+\frac{1}{{n}^{2}}}}$;又$\underset{lim}{n→∞}\frac{1}{\sqrt{1+\frac{1}{n}}}$=1,$\underset{lim}{n→∞}\frac{1}{\sqrt{1+\frac{1}{{n}^{2}}}}$=1.
∴$\underset{lim}{n→∞}$($\frac{1}{\sqrt{{n}^{2}+1}}+\frac{1}{\sqrt{{n}^{2}+2}}+…+\frac{1}{\sqrt{{n}^{2}+n}}$)=1;
(2)∵$\frac{1}{2n}$=$\frac{n}{2{n}^{2}}$≤$\frac{1}{{n}^{2}}+\frac{1}{{(n+1)}^{2}}+…+\frac{1}{{2n}^{2}}$≤$\frac{n}{{n}^{2}}$=$\frac{1}{n}$,$\underset{lim}{n→∞}\frac{1}{2n}$=0,$\underset{lim}{n→∞}$$\frac{1}{n}$=0;
∴$\underset{lim}{n→∞}$($\frac{1}{{n}^{2}}+\frac{1}{{(n+1)}^{2}}+…+\frac{1}{{2n}^{2}}$)=0;
(3)∵$\frac{1+\frac{1}{n}}{2(1+\frac{2}{n})}$=$\frac{1+2+…+n}{{n}^{2}+n+n}$≤$\frac{1}{{n}^{2}+n+1}+\frac{2}{{n}^{2}+n+2}+…+\frac{n}{{n}^{2}+n+n}$≤$\frac{1+2+…+n}{{n}^{2}+n+1}$=$\frac{n(n+1)}{2({n}^{2}+n+1)}$=$\frac{1+\frac{1}{n}}{2(1+\frac{1}{n}+\frac{1}{{n}^{2}})}$.
$\underset{lim}{n→∞}$$\frac{1+\frac{1}{n}}{2(1+\frac{2}{n})}$=$\frac{1}{2}$,$\underset{lim}{n→∞}$$\frac{1+\frac{1}{n}}{2(1+\frac{1}{n}+\frac{1}{{n}^{2}})}$=$\frac{1}{2}$.
∴$\underset{lim}{n→∞}$($\frac{1}{{n}^{2}+n+1}+\frac{2}{{n}^{2}+n+2}+…+\frac{n}{{n}^{2}+n+n}$)=$\frac{1}{2}$.
点评 本题考查了数列极限运算法则、重要极限、数列求和,考查了推理能力与计算能力,属于中档题.

 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案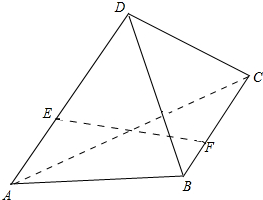 如图,AB和CD是两条异面直线,AB=CD=3,E,F分别为线段AD,BC上的点,且$\frac{AE}{ED}$=$\frac{BF}{FC}$=$\frac{1}{2}$,EF=$\sqrt{7}$,求AB和CD所成的角.
如图,AB和CD是两条异面直线,AB=CD=3,E,F分别为线段AD,BC上的点,且$\frac{AE}{ED}$=$\frac{BF}{FC}$=$\frac{1}{2}$,EF=$\sqrt{7}$,求AB和CD所成的角.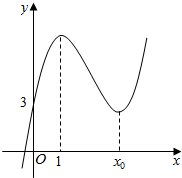 已知函数f(x)=ax3+bx2+(c-3a-2b)x+d(a>0)的图象如图所示,该函数的单调增区间为(-∞,1)和(x0,+∞),单调减区间为(1,x0).
已知函数f(x)=ax3+bx2+(c-3a-2b)x+d(a>0)的图象如图所示,该函数的单调增区间为(-∞,1)和(x0,+∞),单调减区间为(1,x0).