题目内容
14.已知定义域为R的函数g(x),当x∈(-1,1]时,g(x)=$\left\{\begin{array}{l}{\frac{1}{x+1}-1,-1<x≤0}\\{{x}^{2}-3x+2,0<x≤1}\end{array}\right.$,且g(x+2)=g(x)对?x∈R恒成立,若函数f(x)=g(x)-m(x+1)在区间[-1,5]内有6个零点,则实数m的取值范围是( )| A. | ($\frac{2}{5}$,$\frac{2}{3}$) | B. | (-∞,$\frac{2}{5}$]∪($\frac{2}{3}$,+∞) | C. | [$\frac{2}{5}$,$\frac{2}{3}$) | D. | [$\frac{2}{5}$,$\frac{2}{3}$] |
分析 若函数f(x)=g(x)-m(x+1)在区间[-1,5]内有6个零点,则y=g(x)与y=m(x+1)的图象在区间[-1,5]内有6个交点.画出函数的图象,数形结合可得答案.
解答 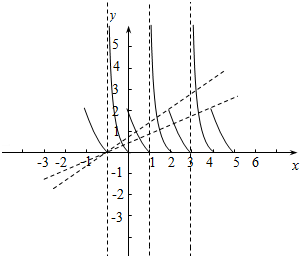 解:∵g(x+2)=g(x)对?x∈R恒成立,
解:∵g(x+2)=g(x)对?x∈R恒成立,
∴函数g(x)的周期为2.
又∵当x∈(-1,1]时,g(x)=$\left\{\begin{array}{l}{\frac{1}{x+1}-1,-1<x≤0}\\{{x}^{2}-3x+2,0<x≤1}\end{array}\right.$,
∴函数g(x)的图象如下图所示:
令函数f(x)=g(x)-m(x+1)=0,
则g(x)=m(x+1),
若函数f(x)=g(x)-m(x+1)在区间[-1,5]内有6个零点,
则y=g(x)与y=m(x+1)的图象在区间[-1,5]内有6个交点.
∵y=m(x+1)恒过点(-1,0),
过(-1,0),(4,2)点的直线斜率为$\frac{2}{5}$,
过(-1,0),(2,2)点的直线斜率为$\frac{2}{3}$,
根据图象可得:x∈[$\frac{2}{5}$,$\frac{2}{3}$),
故选:C.
点评 本题考查的知识点是分段函数的应用,函数的零点,数形结合思想,难度中档.

练习册系列答案
 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
3.已知集合A={x|0<x≤2},B={x|-1<x<$\frac{1}{2}$},则A∪B是( )
| A. | (0,$\frac{1}{2}$) | B. | (0,2) | C. | (-∞,-1]∪(2,+∞) | D. | (-1,2] |