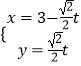题目内容
【题目】已知过原点的动直线![]() 与圆
与圆![]()
![]() 相交于不同的两点
相交于不同的两点![]() .
.
(1)求圆![]() 的圆心坐标;
的圆心坐标;
(2)求线段![]() 的中点
的中点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(3)是否存在实数![]() ,使得直线
,使得直线![]()
![]() 与曲线
与曲线![]() 只有一个交点?若存在,求出
只有一个交点?若存在,求出![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
【答案】(1)![]() ; (2)
; (2)![]() ; (3)
; (3)![]() .
.
【解析】
(1)将方程化为标准式方程,可得到圆心坐标;(2)设线段![]() 的中点,
的中点,![]() 直线
直线![]() 的方程为
的方程为![]() 联立直线和圆的方程得到韦达定理,进而得到
联立直线和圆的方程得到韦达定理,进而得到![]() ,
,![]() ,此时消去参数m即可得到轨迹方程;(3)结合第二问可得到曲线的轨迹,根据直线和圆的位置关系可得到满足题意的结果.
,此时消去参数m即可得到轨迹方程;(3)结合第二问可得到曲线的轨迹,根据直线和圆的位置关系可得到满足题意的结果.
(1)圆![]()
![]() 化为
化为![]() ,所以圆
,所以圆![]() 的圆心坐标为
的圆心坐标为![]()
(2)设线段![]() 的中点,
的中点,![]() 直线
直线![]() 的方程为
的方程为![]() (易知直线
(易知直线![]() 的斜率存在),则
的斜率存在),则![]() 得:
得:![]()
![]() .解得:
.解得:![]()
![]()
![]()
![]() 消去
消去![]() 得:
得:![]()
又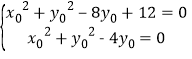 解得:
解得:![]() 或
或![]()
![]()
![]() 的轨迹
的轨迹![]() 的方程为
的方程为![]()
(3)由题意知直线![]() 表示过定点
表示过定点![]()
![]() ,斜率为
,斜率为![]() 的直线.
的直线.
![]() 表示的是一段关于
表示的是一段关于![]() 轴对称,起点为
轴对称,起点为![]() 按顺时针方向运动到
按顺时针方向运动到![]() 的圆弧(不包含端点
的圆弧(不包含端点![]() ).
).
由条件得:![]() 而当直线
而当直线![]() 与轨迹
与轨迹![]() 相切时,
相切时,![]() ,解得
,解得![]() (舍去).
(舍去).
可得当![]() 时,直线
时,直线![]() 与曲线
与曲线![]() 只有一个交点。
只有一个交点。
综上所述,当时![]() 直线
直线![]()
![]() 与曲线
与曲线![]() 只有一个交点.
只有一个交点.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目