题目内容
【题目】三棱柱![]() 中,侧棱与底面垂直,
中,侧棱与底面垂直,![]() ,
,![]() ,
,![]() 分别是
分别是![]() 的中点.
的中点.
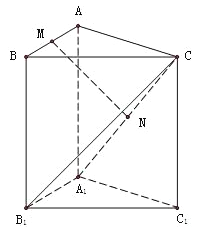
(1)求证:![]() 平面
平面![]() ;
;
(2)求证:![]() 平面
平面![]() ;
;
(3)求二面角![]() 的余弦值.
的余弦值.
【答案】⑴见解析![]() ⑵见解析 ⑶
⑵见解析 ⑶![]()
【解析】
试题(1)证明线面平行,一般利用线面平行判定定理,即从线线平行出发给予证明,而线线平行的寻找与论证往往需要利用平几知识,如本题就利用三角形中位线定理得![]() (2)利用空间向量证明线面垂直,实际就是以算代证,即先求平面的一个法向量,再利用
(2)利用空间向量证明线面垂直,实际就是以算代证,即先求平面的一个法向量,再利用![]() 与法向量关系关系求证(3)求二面角的大小,一般利用空间向量的数量积求解,先建立恰当的空间直角坐标系,设立各点坐标,利用方程组解出各面的法向量,利用向量数量积求法向量的夹角余弦值,最后根据二面角与法向量夹角之间关系求值.
与法向量关系关系求证(3)求二面角的大小,一般利用空间向量的数量积求解,先建立恰当的空间直角坐标系,设立各点坐标,利用方程组解出各面的法向量,利用向量数量积求法向量的夹角余弦值,最后根据二面角与法向量夹角之间关系求值.
试题解析:(1)连接![]() ,
,![]() ,
,
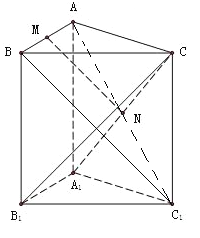
在![]() 中,∵
中,∵![]() 是
是![]() 中点,∴
中点,∴![]() ,
,
又∵![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(2)如图,以![]() 为原点建立空间直角坐标系
为原点建立空间直角坐标系![]() .
.
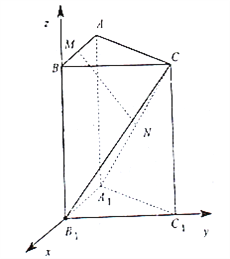
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() .
.
设平面![]() 的法向量
的法向量![]() ,
,
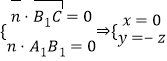 ,
,
令![]() ,则
,则![]() ,
,![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴![]() 平面
平面![]() .
.
(3)设平面![]() 的法向量为
的法向量为![]() ,
,![]() ,
,
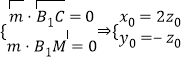 ,
,
令![]() ,则
,则![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
所求二面角![]() 的余弦值为
的余弦值为![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】柴静《穹顶之下》的播出,让大家对雾霾天气的危害有了更进一步的认识,对于雾霾天气的研究也渐渐活跃起来,某研究机构对春节燃放烟花爆竹的天数x与雾霾天数y进行统计分析,得出下表数据:
x | 4 | 5 | 7 | 8 |
y | 2 | 3 | 5 | 6 |
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)试根据(2)求出的线性回归方程,预测燃放烟花爆竹的天数为![]() 的雾霾天数.
的雾霾天数.
