题目内容
【题目】[选修4-4：极坐标与参数方程]
在直角坐标系xOy中，直线l的参数方程为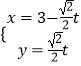 
（t为参数）．在极坐标系（与直角坐标系xOy取相同的长度单位），且以原点O为极点，以x轴正半轴为极轴）中，圆C的方程为ρ=4sinθ．
（1）求圆C的直角坐标方程和直线l普通方程；
（2）设圆C与直线l交于点A，B，若点P的坐标为（3，0），求|PA|+|PB|．
【答案】
（1）解：由ρ=4sinθ，得ρ2=4ρsinθ，
从而可得x2+y2=4y，即x2+y2﹣4y=0，
即圆C的直角坐标方程为x2+（y﹣2）2=4，
直线l的普通方程为x+y﹣3=0
（2）解：将l的参数方程代入圆C的直角坐标方程，
得 
，即 
．
由于 
，
故可设t1，t2是上述方程的两实根，
∴ 
又直线l过点P（3，0），
故由上式及t的几何意义得 
【解析】（1）利用三种方程的转化方法，求圆C的直角坐标方程和直线l普通方程；（2）将l的参数方程代入圆C的直角坐标方程，利用参数的几何意义，即可求|PA|+|PB|．
【题目】已知过原点的动直线
与圆
相交于不同的两点
.
（1）求圆
的圆心坐标；
（2）求线段
的中点
的轨迹
的方程；
（3）是否存在实数
，使得直线
与曲线只有一个交点？若存在，求出
的取值范围；若不存在，说明理由．
【题目】目前，学案导学模式已经成为教学中不可或缺的一部分，为了了解学案的合理使用是否对学生的期末复习有着重要的影响，我校随机抽取100名学生，对学习成绩和学案使用程度进行了调查，统计数据如表所示：
善于使用学案 | 不善于使用学案 | 总计 | |
学习成绩优秀 | 40 | ||
学习成绩一般 | 30 | ||
总计 | 100 |
参考公式： 
，其中n=a+b+c+d．
参考数据：
P（K2≥k0） | 0.050 | 0.010 | 0.001 |
k0 | 3.841 | 6.635 | 10.828 |
已知随机抽查这100名学生中的一名学生，抽到善于使用学案的学生概率是0.6．
（1）请将上表补充完整（不用写计算过程）；
（2）试运用独立性检验的思想方法分析：有多大的把握认为学生的学习成绩与对待学案的使用态度有关？
（3）利用分层抽样的方法从善于使用学案的同学中随机抽取6人，从这6人中抽出3人继续调查，设抽出学习成绩优秀的人数为X，求X的分布列和数学期望．
【题目】某车间为了给贫困山区的孩子们赶制一批爱心电子产品，需要确定加工零件所花费的时间，为此做了四次试验，得到的数据如下表所示：
零件的个数 | 2 | 3 | 4 | 5 |
加工的时间 |
| 3 | 4 |
|
经统计发现零件个数
与加工时间
具有线性相关关系.
（1）求出关于的线性回归方程
；
（2）试预测加工10个零件需要多少时间．
利用公式：
，
