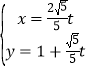Question

【题目】已知直线经过抛物线的焦点且与此抛物线交于，两点，，直线与抛物线交于，两点，且，两点在轴的两侧.

（1）证明：为定值；

（2）求直线的斜率的取值范围；

（3）若（为坐标原点），求直线的方程.

Answer 1

【答案】（1）见解析；（2）；（3）.

【解析】分析：（1）可设l的方程为y=k（x﹣1），k≠0，联立，可得ky2﹣4y﹣4k=0，根据韦达定理即可证明，

（2）根据韦达定理和抛物线的性质可得k2＞1，再联立，得x2﹣kx+k﹣4=0，根据M，N两点在y轴的两侧，可得△=k2﹣4（k﹣4）＞0，即k＜4，即可求出k的范围，

（3）设，，则，，利用根与系数关系表示，即可得到直线的方程.

详解：（1）证明：由题意可得，直线的斜率存在，故可设的方程为，

联立，得，则为定值.

（2）解：由（1）知，， ，

则 ，即.

联立，得，

∵，两点在轴的两侧，∴ ，且，∴.

由及可得或，

故直线的斜率的取值范围为.

（3）解：设，，则，，

∴

，

解得或，又，∴，

故直线的方程为.