题目内容
【题目】选修4-4：坐标系与参数方程
在直角坐标系
中，曲线
的参数方程为
（
为参数，
），曲线
的参数方程为
（
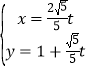为参数，且
）．
（1）以曲线上的点与原点
连线的斜率
为参数，写出曲线的参数方程；
（2）若曲线与的两个交点为
，直线
与直线
的斜率之积为
，求
的值．
【答案】（1）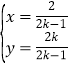
（
为参数，且
）（2）
【解析】分析：（1）将曲线M的参数方程消去参数t，得x﹣2y+2=0（x≠0），由
，得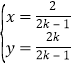
．由此能求出曲线N的参数方程．
（2）曲线M的普通方程为（x﹣2）2+（y﹣1）2=r2，将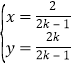代入，得（16﹣4r2）k2+（4r2﹣32）k+17﹣r2=0，由直线OA与直线OB的斜率之积为
，能求出r．
详解：（1）将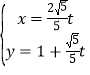
消去参数
，得
.
由
，得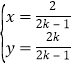
.
故曲线
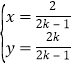的参数方程为（为参数，且）.
（2）曲线
的普通方程为
，
将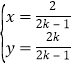代入
并整理得
，
因为直线
与直线
的斜率之积为，所以
，
解得
，又
，所以.
将代入 ，
得
，
，
故.
捷径训练检测卷系列答案
小夫子全能检测系列答案【题目】某学校研究性学习小组调查学生使用智能手机对学习成绩的影响，部分统计数据如下表：
使用智能手机 | 不使用智能手机 | 总计 | |
学习成绩优秀 | 4 | 8 | 12 |
学习成绩不优秀 | 16 | 2 | 18 |
总计 | 20 | 10 | 30 |
（Ⅰ）根据以上
列联表判断，能否在犯错误的概率不超过0.005的前提下认为使用智能手机对学习成绩有影响？
（Ⅱ）从学习成绩优秀的12名同学中，随机抽取2名同学，求抽到不使用智能手机的人数
的分布列及数学期望.
参考公式：
，其中
参考数据：
| 0.05 | 0,。025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】某农科所对冬季昼夜温差大小与某反季大豆新品种发芽多少之间的关系进行了分析研究，分别记录了2016年12月1日至12月5日每天的昼夜温差以及实验室100颗种子中的发芽数，得到的数据如下表所示：
日期 | 12月1日 | 12月2日 | 12月3日 | 12月4日 | 12月5日 |
温差x/℃ | 10 | 11 | 13 | 12 | 8 |
发芽数y/颗 | 23 | 25 | 30 | 26 | 16 |
该农科所确定的研究方案是：先从这五组数据中选取两组，用剩下的三组数据求线性回归方程，再对被选取的两组数据进行检验．
(1)求选取的两组数据恰好是不相邻的两天数据的概率．
(2)若选取的是12月1日和12月5日的两组数据，请根据12月2日至12月4日的数据，求出y关于x的线性回归方程．
(3)由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2，则认为得到的线性回归方程是可靠的，据此说明(2)中所得线性回归方程是否可靠？并估计当温差为9 ℃时，100颗种子中的发芽数．
附：回归方程
中斜率和截距的最小二乘法估计公式分别为：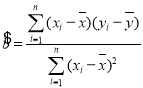
，
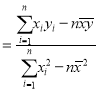