题目内容
【题目】已知二次函数f(x)的图象过点(0,4),对任意x满足f(3﹣x)=f(x),且f(1)=2.
(1)若f(x)在(a,2a﹣1)上单调递减,求实数a的取值范围.
(2)设函数h(x)=f(x)﹣(2t﹣3)x,其中t∈R,求h(x)在区间[0,1]上的最小值g (t).
【答案】(1)a∈(1,![]() ];(2)
];(2)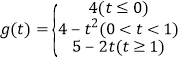
【解析】
(1)由![]() 知,函数的对称轴为
知,函数的对称轴为![]() ,函数在
,函数在![]() 上单调,只需
上单调,只需![]() 即可求解 (2)化简函数
即可求解 (2)化简函数![]() ,根据二次函数的对称轴,分
,根据二次函数的对称轴,分![]() 三种情况讨论,即可求出最小值.
三种情况讨论,即可求出最小值.
(1)设f(x)=ax2+bx+c(a>0),由于过点(0,4),
∴c=4.
由f(3﹣x)=f(x)得,a(3﹣x)2+b(3﹣x)+4=ax2+bx+4,即3a+b=0①
又f(1)=a+b+4=2
∴a=1,b=﹣3,
故f(x)=x2﹣3x+4,
则函数的单调递减区间为:(﹣∞,![]() ]
]
若f(x)在(a,2a﹣1)上单调递减,
则a<2a﹣1≤![]()
解得:a∈(1,![]() ];
];
(2)函数h(x)=f(x)﹣(2t﹣3)x=x2﹣2tx+4的图象是开口朝上,且以直线x=t为对称轴的抛物线,
当t≤0时,h(x)在区间[0,1]上为增函数,当x=0时,h(x)取最小值,即g (t)=h(0)=4.
当0<t<1时,h(x)在区间[0,t]上为减函数,区间[t,1]上为增函数,当x=t时,h(x)取最小值,即g (t)=h(t)=4﹣t2.
当t≥1时,h(x)在区间[0,1]上为减函数,当x=1时,h(x)取最小值,即g (t)=h(1)=5﹣2t.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目