题目内容
5.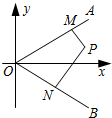 如图,射线OA,OB所在的直线的方向向量分别为$\overrightarrow{d_1}=({1,k})$,$\overrightarrow{d_2}=({1,-k})({k>0})$,点P在∠AOB内,PM⊥OA于M,PN⊥OB于N;
如图,射线OA,OB所在的直线的方向向量分别为$\overrightarrow{d_1}=({1,k})$,$\overrightarrow{d_2}=({1,-k})({k>0})$,点P在∠AOB内,PM⊥OA于M,PN⊥OB于N;(1)若k=1,$P({\frac{3}{2},\frac{1}{2}})$,求|OM|的值;
(2)若P(2,1),△OMP的面积为$\frac{6}{5}$,求k的值;
(3)已知k为常数,M,N的中点为T,且${S_{△MON}}=\frac{1}{k}$,当P变化时,求|OT|的取值范围.
分析 (1)求出|OP|,点P到直线的距离,利用勾股定理,求|OM|的值;
(2)直线OA的方程为kx-y=0,求出P(2,1)到直线的距离,利用勾股定理求出|OM|,利用△OMP的面积为$\frac{6}{5}$,求k的值;
(3)设直线OA的倾斜角为α,求出|OM|,|ON|,利用S△MON=$\frac{1}{k}$,可得P变化时,动点T轨迹方程,求出|OT|,即可求|OT|的取值范围.
解答 解:(1)∵$P({\frac{3}{2},\frac{1}{2}})$,∴|OP|=$\frac{\sqrt{10}}{2}$,
∵OA的方程为y=x,即x-y=0,点P到直线的距离为$\frac{1}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$,
∴|OM|=$\sqrt{\frac{10}{4}-\frac{2}{4}}$=$\sqrt{2}$;
(2)直线OA的方程为kx-y=0,P(2,1)到直线的距离为d=$\frac{|2k-1|}{\sqrt{{k}^{2}+1}}$,
∴|OM|=$\sqrt{5-\frac{(2k-1)^{2}}{{k}^{2}+1}}$,
∴△OMP的面积为$\frac{1}{2}$×$\sqrt{5-\frac{(2k-1)^{2}}{{k}^{2}+1}}$×$\frac{|2k-1|}{\sqrt{{k}^{2}+1}}$=$\frac{6}{5}$,
∴$k=\frac{11}{2}或2$;
(3)设M(x1,kx1),N(x2,-kx2),T(x,y),x1>0,x2>0,k>0,
设直线OA的倾斜角为α,则$k=tanα,sin2α=\frac{2k}{{1+{k^2}}}$,
根据题意得$\left\{\begin{array}{l}x=\frac{{{x_1}+{x_2}}}{2}\\ y=\frac{{k({{x_1}-{x_2}})}}{2}\\|{OM}|={x_1}\sqrt{1+{k^2}}\\|{ON}|={x_2}\sqrt{1+{k^2}}\end{array}\right.⇒\left\{\begin{array}{l}{x_1}=x+\frac{y}{k}\\{x_2}=x-\frac{y}{k}\end{array}\right.$,
代入${S_{△MON}}=\frac{1}{2}|{OM}||{ON}|sin2α=\frac{1}{k}$
化简得动点T轨迹方程为${k^2}{x^2}-{y^2}=1({x≥\frac{1}{k}})$.
∴$|{OT}|=\sqrt{{x^2}+{y^2}}=\sqrt{{x^2}+{k^2}{x^2}-1}=\sqrt{({1+{k^2}}){x^2}-1}≥\sqrt{({1+{k^2}})\frac{1}{k^2}-1}=\frac{1}{k}$,
当且仅当$x=\frac{1}{k},T({\frac{1}{k},0})$时,|OT|取得最小值$\frac{1}{k}$.
∴|OT|的取值范围是$[{\frac{1}{k},+∞})$.
点评 本题考查三角形面积的计算,考查轨迹方程,考查学生分析解决问题的能力,属于中档题.

 同步奥数系列答案
同步奥数系列答案| A. | $\sqrt{2}$ | B. | $\sqrt{10}$ | C. | 2$\sqrt{2}$ | D. | 2 |

| A. | $\frac{140}{3}$π+4$\sqrt{13}$π | B. | 36π+2$\sqrt{13}$π | C. | 32π+2$\sqrt{13}$π | D. | 44π+2$\sqrt{13}$π |
| A. | l∥b | B. | l与b相交 | C. | l与b是异面直线 | D. | l⊥b |
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{8}$ |
 如图,在平面直角坐标系x Oy中,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的离心率为$\frac{{\sqrt{2}}}{2}$,左顶点 A与上顶点 B的距离为$\sqrt{6}$.
如图,在平面直角坐标系x Oy中,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的离心率为$\frac{{\sqrt{2}}}{2}$,左顶点 A与上顶点 B的距离为$\sqrt{6}$.