题目内容
10. 如图,在平面直角坐标系x Oy中,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的离心率为$\frac{{\sqrt{2}}}{2}$,左顶点 A与上顶点 B的距离为$\sqrt{6}$.
如图,在平面直角坐标系x Oy中,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的离心率为$\frac{{\sqrt{2}}}{2}$,左顶点 A与上顶点 B的距离为$\sqrt{6}$.(1)求椭圆C的标准方程;
(2)过原点 O的动直线(与坐标轴不重合)与椭圆C交于 P、Q两点,直线 P A、Q A分别与y轴交于 M、N两点,问以 M N为直径的圆是否经过定点?请证明你的结论.
分析 (1)利用离心率,勾股定理以及椭圆的几何量的关系,列出方程组求解,即可得到椭圆C的标准方程.、
(2)以MN为直径的圆过定点$F(±\sqrt{2},0)$.
设P(x0,y0),则Q(-x0,-y0),P代入椭圆方程,求出直线PA方程,推出$M(0,\frac{{2{y_0}}}{{{x_0}+2}})$;求出直线QA方程,推出$N(0,\frac{{2{y_0}}}{{{x_0}-2}})$;写出以MN为直径的圆的方程,然后化简求出以MN为直径的圆过定点.
解答 (本小题满分14分)
解:(1)由题意得 $\left\{\begin{array}{l}\frac{c}{a}=\frac{{\sqrt{2}}}{2}\\{a^2}+{b^2}=6\\{a^2}-{b^2}={c^2}\end{array}\right.$
解得$a=2,b=\sqrt{2}$
∴椭圆C的标准方程为:$\frac{x^2}{4}+\frac{y^2}{2}=1$.
(2)以MN为直径的圆过定点$F(±\sqrt{2},0)$.
设P(x0,y0),则Q(-x0,-y0),且$\frac{x_0^2}{4}+\frac{y_0^2}{2}=1$,即$x_0^2+2y_0^2=4$,
∵A(-2,0),∴直线PA方程为:$y=\frac{y_0}{{{x_0}+2}}(x+2)$,∴$M(0,\frac{{2{y_0}}}{{{x_0}+2}})$;
∴直线QA方程为:$y=\frac{y_0}{{{x_0}-2}}(x+2)$,∴$N(0,\frac{{2{y_0}}}{{{x_0}-2}})$;
以MN为直径的圆为:$(x-0)(x-0)+(y-\frac{{2{y_0}}}{{{x_0}+2}})(y-\frac{{2{y_0}}}{{{x_0}-2}})=0$,
即${x^2}+{y^2}-\frac{{4{x_0}{y_0}}}{{{x_0}^2-4}}y+\frac{{4{y_0}^2}}{{{x_0}^2-4}}=0$,
∵$x_0^2-4=-2y_0^2$,∴${x^2}+{y^2}+\frac{{2{x_0}}}{y_0}y-2=0$,
令y=0,得x2-2=0,解得:$x=±\sqrt{2}$,
∴以MN为直径的圆过定点:$F(±\sqrt{2},0)$.
点评 本题考查椭圆的方程的求法,椭圆的综合应用,直线与圆的位置关系的应用,考查分析问题解决问题的能力.

 阅读快车系列答案
阅读快车系列答案| A. | $\frac{\sqrt{3}π}{18}$ | B. | $\frac{\sqrt{3}π}{12}$ | C. | $\frac{\sqrt{3}π}{9}$ | D. | $\frac{\sqrt{3}π}{6}$ |
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | $\frac{2}{3}$ |
| A. | 8 | B. | 7 | C. | 4 | D. | 3 |
| A. | x=$\frac{π}{3}$ | B. | x=-$\frac{π}{6}$ | C. | x=-$\frac{π}{24}$ | D. | x=$\frac{11π}{24}$ |
| A. | 3 | B. | 4 | C. | 7 | D. | 8 |
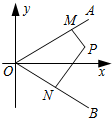 如图,射线OA,OB所在的直线的方向向量分别为$\overrightarrow{d_1}=({1,k})$,$\overrightarrow{d_2}=({1,-k})({k>0})$,点P在∠AOB内,PM⊥OA于M,PN⊥OB于N;
如图,射线OA,OB所在的直线的方向向量分别为$\overrightarrow{d_1}=({1,k})$,$\overrightarrow{d_2}=({1,-k})({k>0})$,点P在∠AOB内,PM⊥OA于M,PN⊥OB于N; 如图所示,曲线C由上半圆C1:x2+y2=1(y≥0)和部分抛物线C2:y=x2-1(y≥0)连接而成,A,B为C1与C2的公共点(B在原点右侧),过C1上的点D(异于点A,B)的切线l与C2分别相交于M,N两点.
如图所示,曲线C由上半圆C1:x2+y2=1(y≥0)和部分抛物线C2:y=x2-1(y≥0)连接而成,A,B为C1与C2的公共点(B在原点右侧),过C1上的点D(异于点A,B)的切线l与C2分别相交于M,N两点.