题目内容
17.某几何体的三视图如图所示,则此几何体的表面积为( )
| A. | $\frac{140}{3}$π+4$\sqrt{13}$π | B. | 36π+2$\sqrt{13}$π | C. | 32π+2$\sqrt{13}$π | D. | 44π+2$\sqrt{13}$π |
分析 首先根据三视图把该几何体的复原图整理出来,进一步利用立体图的相关的数据求出结果.
解答 解:根据三视图得知:
该几何体是由下面是一个半径为4的半球,上面是一个底面半径为2,高为3的圆锥构成的组合体.
首先求出上面圆锥的侧面展开面的半径r=$\sqrt{13}$
圆锥的底面周长为l=4π,
所以圆锥的侧面面积为:s1=$\frac{1}{2}•4π•\sqrt{13}=2\sqrt{13}π$,
剩余的侧面面积为:s2=2π•16+16π-4π=44π,
所以组合体的侧面面积为:s=s1+s2=44π+2$\sqrt{13}π$
故选:D
点评 本题考查的知识要点:三视图与立体图形之间的转换,组合图的侧面展开图的侧面积的求法.主要考查学生的空间想象能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.将函数f(x)=$\sqrt{3}$cos2$\frac{x}{2}$+$\frac{1}{2}$sinx-$\frac{\sqrt{3}}{2}$的图象上所有点的纵坐标不变,横坐标变为原来的$\frac{1}{2}$,再将所得图象向右平移$\frac{π}{3}$得到函数g(x),则函数g(x)的解析式为( )
| A. | g(x)=cos$\frac{x}{2}$ | B. | g(x)=-sin2x | C. | g(x)=sin(2x-$\frac{π}{3}$) | D. | g(x)=sin($\frac{x}{2}$+$\frac{π}{6}$) |
6.若复数z满足(2+i)z=1+2i(i是虚数单位),则z的共轭复数所对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
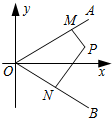 如图,射线OA,OB所在的直线的方向向量分别为$\overrightarrow{d_1}=({1,k})$,$\overrightarrow{d_2}=({1,-k})({k>0})$,点P在∠AOB内,PM⊥OA于M,PN⊥OB于N;
如图,射线OA,OB所在的直线的方向向量分别为$\overrightarrow{d_1}=({1,k})$,$\overrightarrow{d_2}=({1,-k})({k>0})$,点P在∠AOB内,PM⊥OA于M,PN⊥OB于N; 图中,x1,x2,x3为某次考试三个评阅人对同一道题的独立评分,P为该题的最终得分.当输入x1=7,x2=10时,输出P=7.5,则输入x3的值应为( )
图中,x1,x2,x3为某次考试三个评阅人对同一道题的独立评分,P为该题的最终得分.当输入x1=7,x2=10时,输出P=7.5,则输入x3的值应为( ) 如图,已知四棱锥P-ABCD中,侧面PAD⊥底面ABCD,AB∥CD,AD⊥CD,PA=PD=CD=2AB=2.
如图,已知四棱锥P-ABCD中,侧面PAD⊥底面ABCD,AB∥CD,AD⊥CD,PA=PD=CD=2AB=2.