题目内容
13．求证：（${C}_{n}^{0}$）2+（${C}_{n}^{1}$）2+…+（${C}_{n}^{n}$）2=${C}_{2n}^{n}$．分析 由（1+x）n（1+x）n=（1+x）2n，通过二项式定理，两边展开得，再根据组合数公式的性质，化简即可．
解答 证明：由（1+x）n（1+x）n=（1+x）2n，两边展开得：
（Cn0+Cn1x+Cn2x2+…+Cnm-1xn-1+Cnnxn）•（Cn0+Cn1x+Cn2x2+…+Cnn-1xn-1+Cnnxn）=C2n0+C2n1x+C2n1x2+…+C2n2nx2n
比较等式两边xn的系数，它们应当相等，所以有：
Cn0•Cnn+Cn1•Cnn-1+Cn2•Cnn-2+…+Cnn•Cn0=C2nn
由Cnr=Cnn-r，
得（Cn0）2+（Cn1）2+（Cn2）2+…+（Cnn）2=C2nn．
点评 本题考查了组合及组合数公式，以及二项式展开定理，属于基础题．
练习册系列答案
期末集结号系列答案
相关题目
4．已知复数z：满足（1+$\sqrt{3}$i）z=1+i，则|z|等于（ ）
| A． | $\frac{\sqrt{2}}{2}$ | B． | -$\sqrt{2}$ | C． | $\sqrt{2}$ | D． | 2 |
1．若两曲线y=x2与y=cx3（c＞0）所围成的图形面积为$\frac{2}{3}$，则c=（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{1}{2}$ | C． | 1 | D． | $\frac{2}{3}$ |
18．设集合M={x|x2-2x-3＜0，x∈Z}，则集合M的真子集个数为（ ）
| A． | 8 | B． | 7 | C． | 4 | D． | 3 |
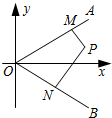如图，射线OA，OB所在的直线的方向向量分别为$\overrightarrow{d_1}=（{1，k}）$，$\overrightarrow{d_2}=（{1，-k}）（{k＞0}）$，点P在∠AOB内，PM⊥OA于M，PN⊥OB于N；